Question

Точка М - середина отрезка АВ, причем точка А лежит в плоскости , а через точки В и середину М отрезка АВ проведены параллельные прямые, пересекающие плоскость α в некоторых точках В1 и М1 соответственно. Найдите длину отрезка ММ1, если ВВ1=17м, . (Указание: применить теорему о средней линии треугольника и теорему Фалеса)

Answer 1

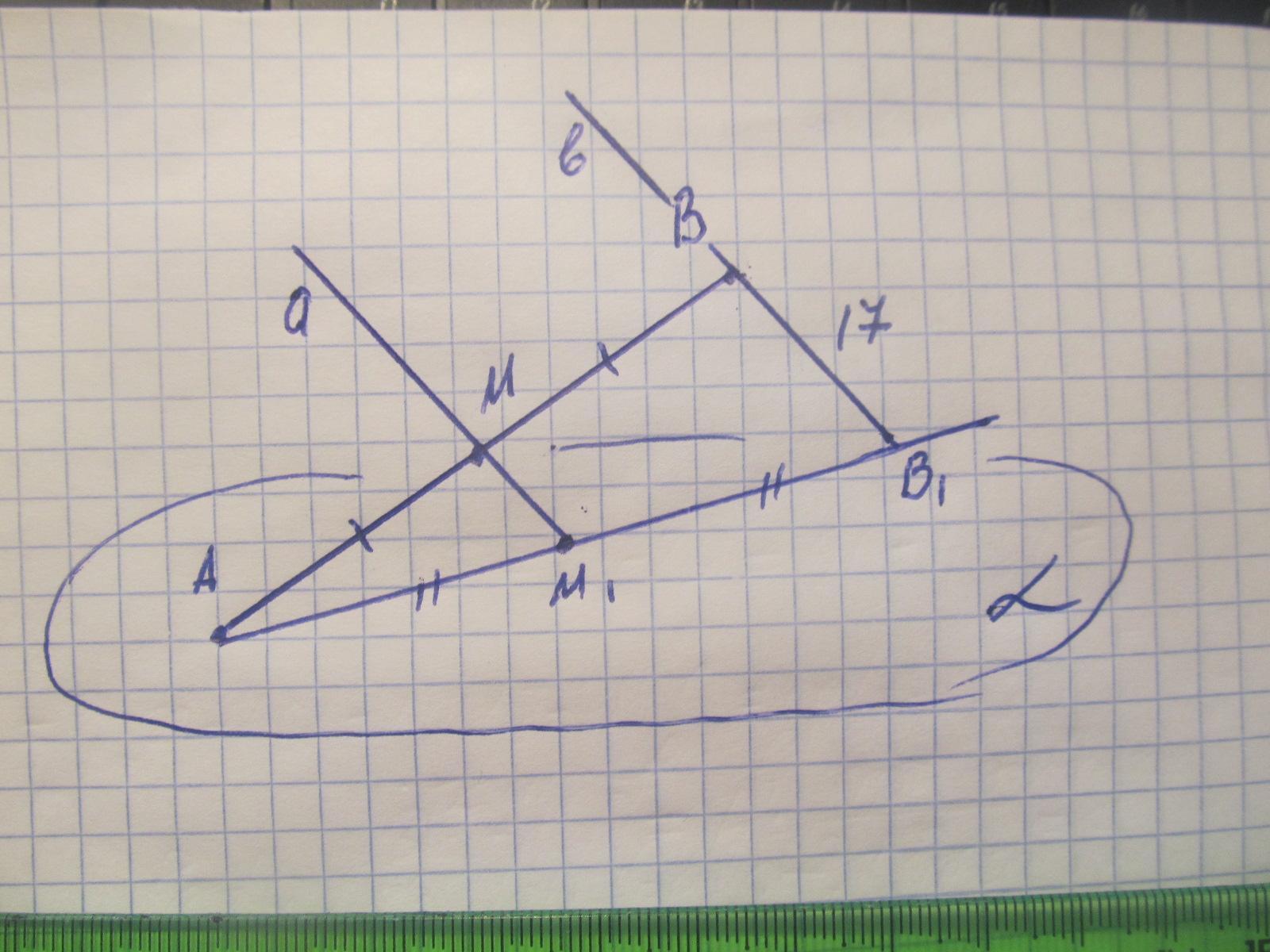
Дано: отрезок АВ; АМ=МВ; прямые а и в параллельны.

т.М ∈ а; т.В ∈ в;   т.т. А, М1 и В1 ∈ α; ВВ1=17 м; ММ1 - ?

------------------------------------------------------------------------------

1) Рассм. ∠ВАВ1.  По т. Фалеса при АМ=МВ и а║в  АМ1=М1В1.

2) Рассм. Δ АВВ1; АМ=МВ;  АМ1=М1В1  ⇒

ММ1 - средняя линия Δ АВВ1.    Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.

ММ1=1/2 * ВВ1

ММ1=1/2 * 17=8,5 м  -  это ответ.