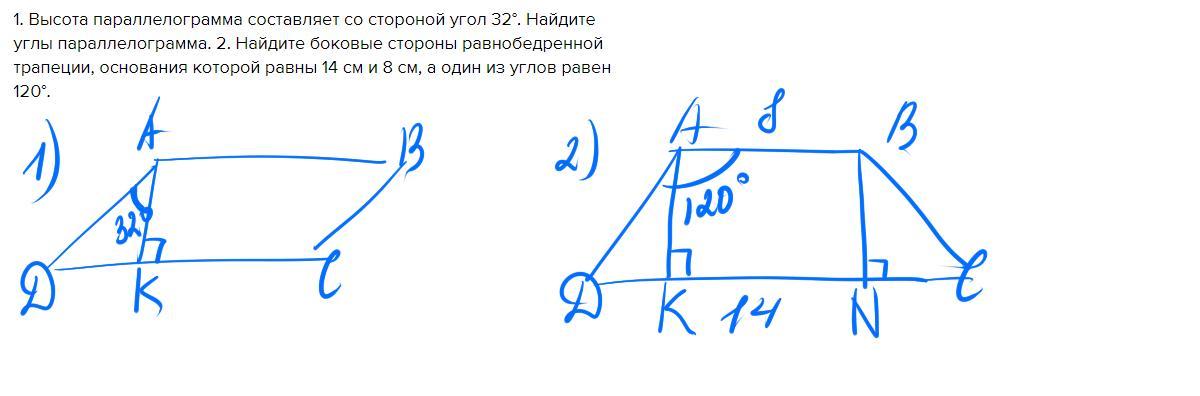
1. Высота параллелограмма составляет со стороной угол 32°. Найдите углы параллелограмма. 2. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120°.
Ответы
1. На рисунке ABCD — параллелограмм. AK⊥DC ==> ∠AKD=90°. По условию ∠DAK=32° ==> ∠ADC=90°-32°=58°.
В параллелограмме противоположные углы равны, значит ∠ADC=∠ABC=32°, а ∠DAB=∠BCD=180°-∠ADC=180°-32°=148°.
Ответ: 32°, 148°, 32°, 148°.
2. На рисунке ABCD — равнобедренная трапеция, AB║CD, BC=AD, AB=8 см, DC=14 см, ∠DAB=120°. Проведем AK⊥DC и BN⊥DC. ABNK — прямоугольник, так как все его углы = 90°.
ΔADK = ΔBCN за гипотенузой и острым углом (углы при основе равнобедренной трапеции равны). Значит DC=DK+KN+NC=2DK+AB (так как AB=KN). ==> DK=(DC-AB):2=(14-8):2=6:2=3 (см).
В ΔADK ∠K=90°, ∠D=180°-120°=60° (как внутренний односторонний угол при AB║DC и AD-секущей), значит ∠A=30°. DK-катет, который лежит против угла в 30°, значит AD=2DK=2*6=12 (см)
АD=BC=12 (см) как боковые стороны равнобедренной трапеции.
Ответ: 12 см, 12 см.