Скоротіть дріб:
х¹¹+х¹⁰+х⁹+х⁸+х⁷+х⁶+х⁵+х⁴+х³+х²+х+1
----------------------------------------------------
(х³+1)(х⁶+1)
Приложения:
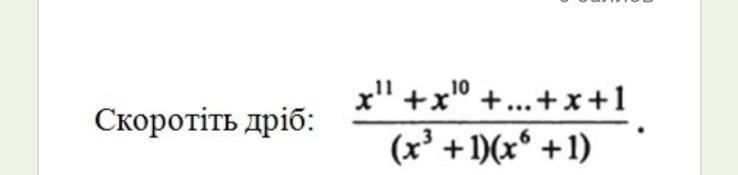
Ответы
Ответ дал:
9
Аноним:
спасибо большое у меня 5
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад