Предмет: Геометрия
Автор: nKrynka
Вопрос задан 3 года назад

Помогите, пожалуйста, решить задачу: В тетраэдре АВСD точки К,М,Р – середины отрезков АВ,ВС, СD, - соответственно. Определите вид сечения тетраэдра плоскостью (КМР). Докажите, что (КМР) ǁ АС, (КМР) ǁ ВD. (С рисунком, пожалуйста)

Simba2017: А-вершина?

Simba2017: параллелограмм

Simba2017: прямоугольник-это его частный случай

Simba2017: КМ-средняя линия грани АВС, значит она параллельна АС

Simba2017: ну а если прямая, не лежащая в плоскости (АС) параллельна прямой плоскости (КМ) , то такие прямая и плоскость параллельны

Simba2017: аналогично рассуждая про KF и плоскость

Simba2017: РМ-средняя линия грани ВСD, параллельна BD значит

Simba2017: если тетраэдр правильный, все грани правильные треугольники-то в сечении прямо даже квадрат выйдет

Simba2017: средние линии всех граней равны будут в этом случае

Simba2017: но в задании этого нет, значит в сечении параллелограмм, четырехугольник-у которого противоположные стороны параллельны

Ответы

Ответ дал: Simba2017

К и М лежат в одной грани АВС, соединяю их прямой-это средняя линия треугольника, поэтому KM||AC

Аналогично Р и М в нижней грани BCD -соединяю, PM||DB

так как линии сечения параллельны ребрам-провожу из точки Р прямую параллельно АС, получаю точку F-пересечения прямой и ребра AD

полученный четырехугольник -параллелограмм, так как стороны его КМ и PF параллельны АС, а стороны KF и PM параллельны BD

Ну а параллельность плоскости сечения ребрам следует из теоремы

Если прямая вне плоскости параллельна прямой в плоскости, то прямая и плоскость параллельны ( или еще пишут-не имеют общих точек)

Приложения:

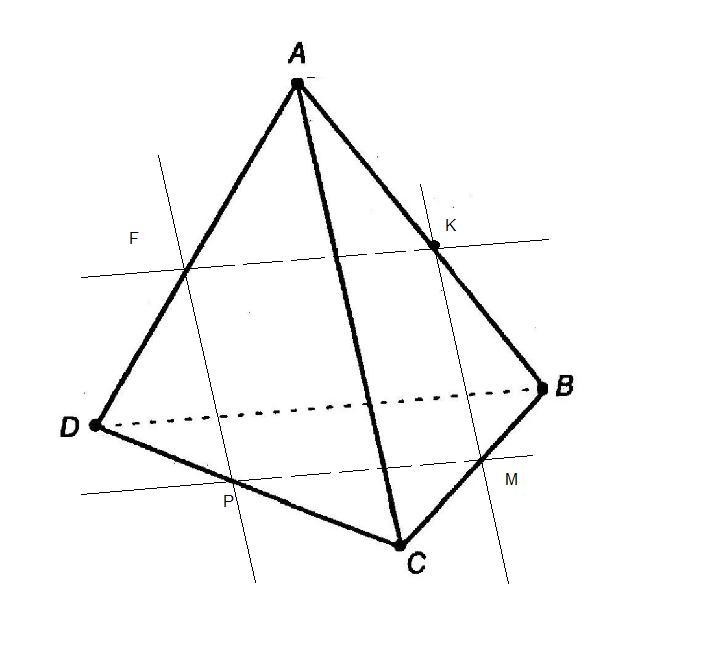
Simba2017: так как через две параллельные прямые Км и PF проходит единственная плоскость

Simba2017: если у нас две единственные плоскости сечения через точки К,М,Р, то они совпадают эти плоскости-это и есть искомое сечение

nKrynka: Вот, я и не делала дополнительных построений. Я ломала голову, как провести сечение через три заданные точки. А теперь мне всё стало понятно. Благодарю Вас.

Simba2017: обращайтесь если что, уж вам то всегда помогу)

nKrynka: Сейчас почему - то нельзя писать в личку. Я хотела к Вам обратиться за помощью напрямую. Но, написали, что нельзя.

Simba2017: странно, я пишу многим

Simba2017: сайт барахлит еще

nKrynka: Вот так пишут: Мы отключили личные сообщения и комментарии в профилях.

Simba2017: у меня сайт есть, пишите туда

nKrynka: Спасибо.

Вас заинтересует

Английский язык

2 года назад

пожалуйста помогите срочно надо!!! Даю 30 балов срочно!!!!!

Английский язык