Question

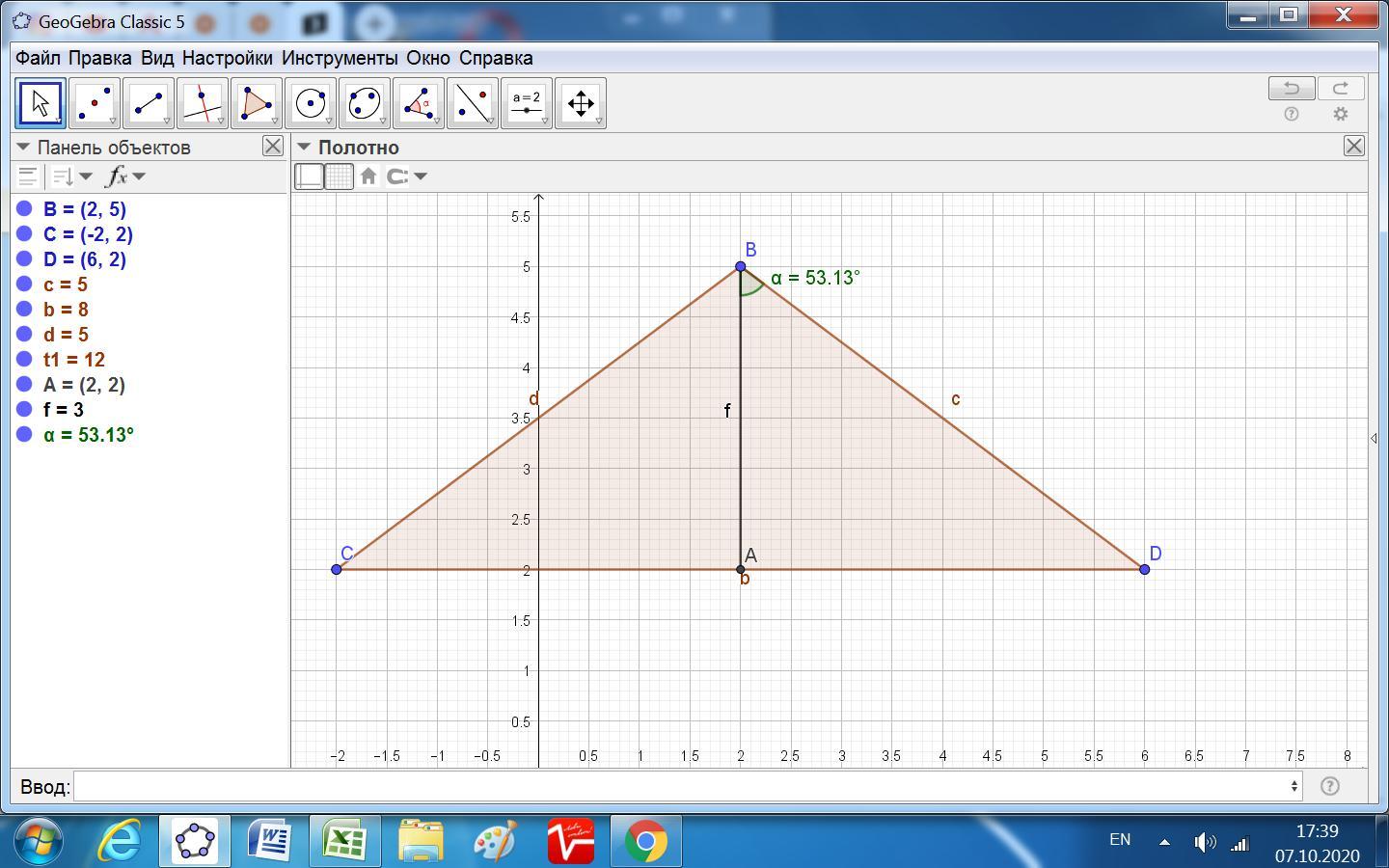
3. В треугольнике ВСD с координатами вершин В(2,5), С(-2;2), D(6;2) проведена медиана ВА.

а) найдите угол между векторами ВА и ВD

б) найдите длину вектора ВА

​

Answer 1

В треугольнике ВСD с координатами вершин В(2,5), С(-2;2), D(6;2) проведена медиана ВА.

а) найдите угол между векторами ВА и ВD

б) найдите длину вектора ВА .

а) Находим векторы ВА и ВD.

Для этого сначала определяем координаты точки А как середины стороны СD: С(-2;2), D(6;2).

А(((-2+6)/2); ((2+2)/2)) = (2; 2).

Определяем вектор ВА. Точка В(2,5).

ВА = (2-2; 2-5) = (0; -3). Модуль равен √(0² + (-3)²) = 3. Это его длина.

Определяем вектор ВD. Точки В(2,5) и D(6;2).

ВD = (6-2; 2-5) = (4; -3). Модуль равен √(4² + (-3)²) = 5.

cos(ВА_ВD) =  (0*4 + (-3)*(-3)) / (3*5) = 9/15 = 3/5 = 0,6.

Угол равен arc cos 0,6 = 0,927295 радиан или 53,1301 градуса.

б) Длина вектора ВА  определена ранее: |BA| = 3.