Задание 3 (30 баллов).
Выполните действия:
Задание 4 (30 баллов).
Докажите, что при всех допустимых значениях переменных значение выражения не зависит от значения переменных:
Приложения:
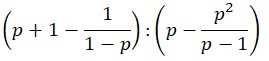
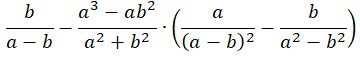
Ответы
Ответ дал:
27
Ответ:
Объяснение:
3.
4.
1) Упростим выражение в скобках:
2)
3)
senk84:
Я Вас обожаю СПАСИБО!!!!
Удачи.
удачи
а в 4 точно всё надо переписывать
удачи всем, кто видит этот комментарий !
И вам
Благодарю
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад