Question

СРОЧНО ДАЮ 40 БАЛЛОВ
ИЗОБРАЗИТЕ МНОЖЕСТВО ТОЧЕК,ЗАДАННЫХ СИСТЕМОЙ НЕРАВЕНСТВ
$x { }^{2} + y {}^{2} \leqslant 36 \\ xy > 4$
​

Answer 1

$\left\{\begin{array}{l}x^2+y^2\leq 36\\xy>4\end{array}\right\ \ \ \left\{\begin{array}{l}x^2+y^2\leq 6^2\\y>\dfrac{4}{x}\ ,\ esli\ x>0\\\ y<\dfrac{4}{x}\ ,\ esli\ x<0\end{array}\right$

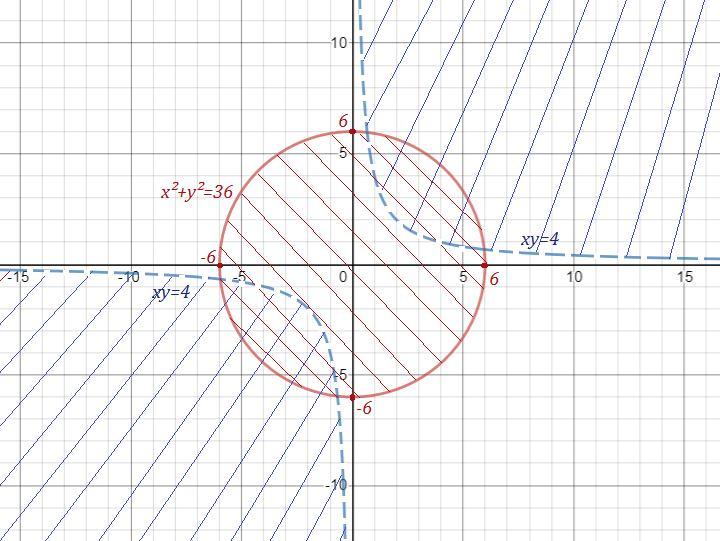
x²+y²≤ 36 -  эта область-  круг с центром (0,0) и R=6 , граница входит в область . Красная штриховка .

xy=4  - это гипербола. Область xy>4  при  х>0 (в правой полуплоскости) лежит выше линии гиперболы. Область ху>4 при х <0 (в левой полуплоскости) лежит ниже линии гиперболы. Граница не входит в область . Синяя штриховка .

На рисунке искомая область заштрихована пересечением синих и красных линий.