Question

Дан треугольник ABC. Известно, что AB = 6, BC = 4
, ∠ABC = 30°. Найди длину медианы BD. Реши задачу, применяя векторы.
Ответ:
​

Answer 1

Ответ:

$\boxed{BD = \sqrt{13 + 6\sqrt{3}}}$

Пошаговое объяснение:

Дано: AB = 6, BC = 4, ∠ABC = 30°, AD = CD

Найти: BD - ?

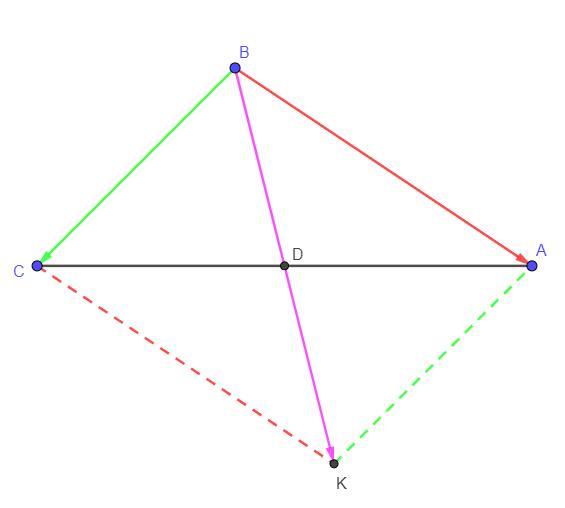
Решение: Пусть BC и BA - векторы, то есть введем векторы: $\overrightarrow{BC}, \overrightarrow{BA}.$ Сложим векторы $\overrightarrow{BC}$ и $\overrightarrow{BA}$ по правила параллелограмма. Для этого достроим треугольник ΔABC до параллелограмма. Продлим медиану BD до луча BD. На луче BD отметим такую точку K, что BD = DK. Тогда ABCK - параллелограмм по теореме-признаку, так как AD = CD по условию и BD = DK по построению, тогда диагонали четырехугольника ABCK - делятся пополам, следовательно данный четырехугольник - параллелограмм.

По правилу параллелограмма:

$\overrightarrow{BC} + \overrightarrow{BA} = \overrightarrow{BK}$

$(\overrightarrow{BC} + \overrightarrow{BA})^{2} = \overrightarrow{BK}^{2}$

$\overrightarrow{BC}^{2} + \overrightarrow{BA}^{2} + 2\cdot\overrightarrow{BC}\cdot\overrightarrow{BA} = \overrightarrow{BK}^{2}$

$|\overrightarrow{BC}|^{2} + |\overrightarrow{BA}|^{2} + 2\cdot\overrightarrow{BC}\cdot\overrightarrow{BA} =| \overrightarrow{BK}|^{2}$

$|\overrightarrow{BC}|^{2} + |\overrightarrow{BA}|^{2} + 2\cdot |\overrightarrow{BC}|\cdot|\overrightarrow{BA}| \cdot \cos\angle(\overrightarrow{BC},\overrightarrow{BA}) =| \overrightarrow{BK}|^{2}$

$\sqrt{ | \overrightarrow{BK}|^{2}} = \sqrt{ |\overrightarrow{BC}|^{2} + |\overrightarrow{BA}|^{2} + 2\cdot |\overrightarrow{BC}|\cdot|\overrightarrow{BA}| \cdot \cos\angle(\overrightarrow{BC},\overrightarrow{BA}) }$

$| \overrightarrow{BK}| = \sqrt{ |\overrightarrow{BC}|^{2} + |\overrightarrow{BA}|^{2} + 2\cdot |\overrightarrow{BC}|\cdot|\overrightarrow{BA}| \cdot \cos\angle(\overrightarrow{BC},\overrightarrow{BA}) } =$

$= \sqrt{ 4^{2} + 6^{2} + 2\cdot 4\cdot6 \cdot \cos(30^{\circ}) } = \sqrt{16 + 36 + 2 \cdot 4 \cdot 6 \cdot \dfrac{\sqrt{3} }{2} } = \sqrt{52 + 24\sqrt{3} } =$

$= \sqrt{4 * 13 + 4 * 6\sqrt{3} }= \sqrt{4 * (13 + 6\sqrt{3}) } = 2\sqrt{13 + 6\sqrt{3}}$.

Так как по построению D - середина отрезка BK, то

$BD = \dfrac{| \overrightarrow{BK}|}{2} = \dfrac{2\sqrt{13 + 6\sqrt{3}}}{2} =\sqrt{13 + 6\sqrt{3}}$.