Question

abcd параллелограмм bk биссектриса bk=6 см kd=2см найдите периметр BCDK

Срочно пж

Answer 1

Полное условие:

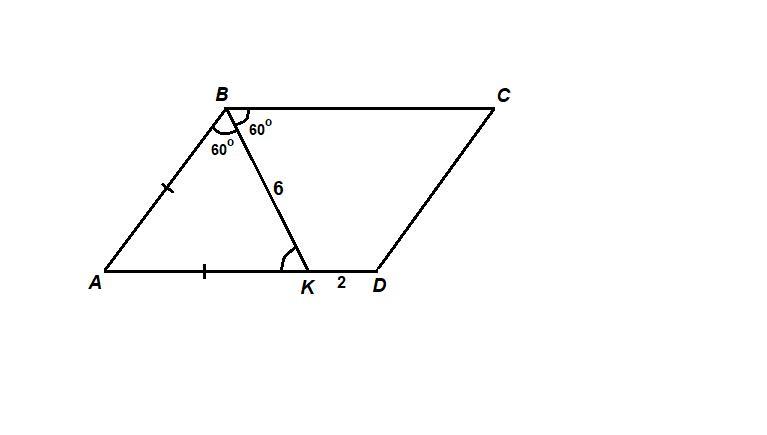
АВСD - параллелограмм, ВК - биссектриса, ВК = 6 см, КD = 2 см, ∠АВК = ∠КВС=60°.

Найти периметр ВСDК.

Ответ:

22 см

Объяснение:

∠AKB = ∠КВС = 60° как накрест лежащие при пересечении параллельных прямых ВС и AD секущей ВК.

∠АВК = ∠КВС=60° по условию, значит

∠AKB = ∠АВК = 60°, следовательно ΔАВК равнобедренный с основанием ВК. А так как у него есть углы по 60°, то он равносторонний.

АВ = АК = ВК = 6 см

AD = AK + KD = 6 + 2 = 8 см

Противоположные стороны параллелограмма равны. Поэтому:

BC = AD = 8 см

CD = AB = 6 см

$P_{BCDK}=BC+CD+DK+BK=8+6+2+6=22$ см