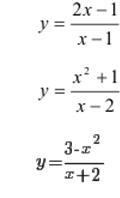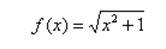Question

30 баллов! Найти асимптоты функций и построить графики

Answer 1

Прямую называют асимптотой графика функции, если расстояние между этой прямой и точкой графика стремится к нулю при отдалении этой точки от начала координат.

Асимптоты бывают вертикальными, горизонтальными и наклонными.

Если существует такое число $a$, что $\displaystyle \lim_{x \to a} f(x) = \infty$, то $x=a$ — вертикальная асимптота графика функции $y=f(x).$

Если имеем функцию $y=f(x)$, для которой существуют $\displaystyle \lim_{x \to \infty} \frac{f(x)}{x}$ и $\displaystyle \lim_{x \to \infty} (f(x)-kx)$, причем $\displaystyle \lim_{x \to \infty} \frac{f(x)}{x} = k$ и $\displaystyle \lim_{x \to \infty} (f(x)-kx) = b$, то прямая $y = kx + b$ при $k \neq 0$ является наклонной асимптотой графика функции $y=f(x)$, а при $k = 0$ — горизонтальной асимптотой, уравнение которой $y = b.$

$1) ~ f(x) = \dfrac{2x - 1}{(x-1)^{2}}$

$D(f): ~ x \neq 1$

Поскольку в точке $x = 1$ функция имеет разрыв, то прямая $x=1$ может оказаться вертикальной асимптотой. Имеем:

$\displaystyle \lim_{x \to 1} \dfrac{2x - 1}{(x-1)^{2}} = \dfrac{2 \cdot 1 - 1}{(1 - 1)^{2}} = \infty$

Следовательно, $x = 1$ — вертикальная асимптота.

Имеем далее:

$\displaystyle \lim_{x \to \infty} \frac{f(x)}{x} = \lim_{x \to \infty} \dfrac{\dfrac{2x - 1}{(x-1)^{2}}}{x} = \lim_{x \to \infty}\dfrac{2x-1}{x(x-1)^{2}} = \lim_{x \to \infty} \dfrac{2x}{x^{3}} = 0$

Поскольку $k=0$, то если асимптота существует, то она будет горизонтальной асимптотой.

$\displaystyle \lim_{x \to \infty} \left(f(x)-kx \right) = \lim_{x \to \infty} \left(\dfrac{2x - 1}{(x-1)^{2}}-0 \cdot x \right) = \lim_{x \to \infty} \dfrac{2x - 1}{(x-1)^{2}} =\\\\= \lim_{x \to \infty} \dfrac{2x}{x^{2}} = 0$

Итак, имеем уравнение горизонтальной асимптоты: $y=0$

$2) ~ y = \dfrac{2x - 1}{x - 1}$

$D(f): ~ x \neq 1$

$\displaystyle \lim_{x \to 1} \dfrac{2x - 1}{x-1} = \dfrac{2 \cdot 1 - 1}{1 - 1} = \infty$

$x = 1$ — вертикальная асимптота.

$\displaystyle \lim_{x \to \infty} \frac{f(x)}{x} = \lim_{x \to \infty} \dfrac{\dfrac{2x - 1}{(x-1)}}{x} = \lim_{x \to \infty}\dfrac{2x-1}{x(x-1)} = \lim_{x \to \infty} \dfrac{2x}{x^{2}} = 0$

$\displaystyle \lim_{x \to \infty} \left(f(x)-kx \right) = \lim_{x \to \infty} \left(\dfrac{2x - 1}{x-1}-0 \cdot x \right) = \lim_{x \to \infty} \dfrac{2x - 1}{x-1} =\\\\= \lim_{x \to \infty} \dfrac{2x}{x} = 2$

$y=2$ — горизонтальная асимптота.

$3) ~ y = \dfrac{x^{2} + 1}{x-2}$

$D(f): ~ x \neq 2$

$\displaystyle \lim_{x \to 2} \frac{x^{2} + 1}{x-2} = \frac{2^{2} + 1}{2 - 2} = \infty$

$x = 2$ — вертикальная асимптота.

$\displaystyle \lim_{x \to \infty} \frac{f(x)}{x} = \lim_{x \to \infty} \dfrac{\dfrac{x^{2} + 1}{x-2}}{x} = \lim_{x \to \infty} \frac{x^{2} + 1}{x(x-2)} = \lim_{x \to \infty} \frac{x^{2}}{x^{2}} = 1$

$\displaystyle \lim_{x \to \infty} \left(f(x)-kx \right) = \lim_{x \to \infty} \left(\frac{x^{2} + 1}{x-2}-1 \cdot x \right) = \lim_{x \to \infty} \frac{2x + 1}{x - 2} = \\\\=\lim_{x \to \infty} \frac{2x}{x} = 2$

$y=x+2$ — наклонная асимптота.

$4) ~ y = \dfrac{3 - x^{2}}{x + 2}$

$D(f): ~ x \neq -2$

$\displaystyle \lim_{x \to -2} \dfrac{3 - x^{2}}{x + 2} = \frac{3 - (-2)^{2}}{-2 + 2} = \infty$

$x = -2$ — вертикальная асимптота.

$\displaystyle \lim_{x \to \infty} \frac{f(x)}{x} = \lim_{x \to \infty} \dfrac{\dfrac{3 - x^{2}}{x + 2}}{x} = \lim_{x \to \infty} \frac{3 - x^{2}}{x(x+2)} = \lim_{x \to \infty} \frac{-x^{2}}{x^{2}} = -1$

$\displaystyle \lim_{x \to \infty} \left(f(x)-kx \right) = \lim_{x \to \infty} \left(\dfrac{3 - x^{2}}{x + 2}- (-1) \cdot x \right) = \lim_{x \to \infty} \frac{2x + 3}{x + 2} = \\\\=\lim_{x \to \infty} \frac{2x}{x} = 2$

$y=-x+2$ — наклонная асимптота.

$5) ~ f(x) = \sqrt{x^{2} + 1}$

$D(f) = (-\infty; ~ {+}\infty)$

Нет вертикальных асимптот.

$\displaystyle \lim_{x \to \infty} \frac{f(x)}{x} = \lim_{x \to \infty} \dfrac{\sqrt{x^{2} + 1}}{x} = \lim_{x \to \infty} \frac{|x|}{x} = \pm 1$

$\text{I}) ~ \displaystyle \lim_{x \to {+}\infty} \left(f(x)-kx \right) = \lim_{x \to {+}\infty} \left(\sqrt{x^{2} + 1}- x \right) = ({+}\infty - \infty) = \\\\= \lim_{x \to {+}\infty} \frac{(\sqrt{x^{2} + 1}- x)(\sqrt{x^{2} + 1}+x)}{\sqrt{x^{2} + 1}+ x} = \lim_{x \to {+}\infty} \frac{x^{2} + 1 - x^{2}}{\sqrt{x^{2} + 1}+ x} =\\\\= \lim_{x \to {+}\infty} \frac{1}{\sqrt{x^{2} + 1}+ x} = 0$

$\text{II}) ~ \displaystyle \lim_{x \to {-}\infty} \left(f(x)-kx \right) = \lim_{x \to {-}\infty} \left(\sqrt{x^{2} + 1}+ x \right) = ({+}\infty - \infty) = \\\\= \lim_{x \to {-}\infty} \frac{(\sqrt{x^{2} + 1}+ x)(\sqrt{x^{2} + 1}-x)}{\sqrt{x^{2} + 1}- x} = \lim_{x \to {-}\infty} \frac{1}{\sqrt{x^{2} + 1}- x} = 0$

$y=x$ и $y = -x$ — наклонные асимптоты.