Умоляю помогите!! 40 баллов и больше!
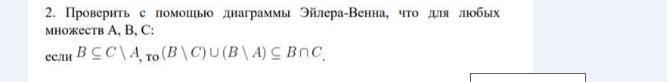
Ответы
Проверить с помощью диаграммы Эйлера-Венна, что для любых множеств А, В, С: если
B ⊆ C\A, то (B\C) ∪ (B\A) ⊆ (B∩C)
=========================================
Разность множеств C\A состоит из всех элементов множества С, которые не являются элементами множества А.
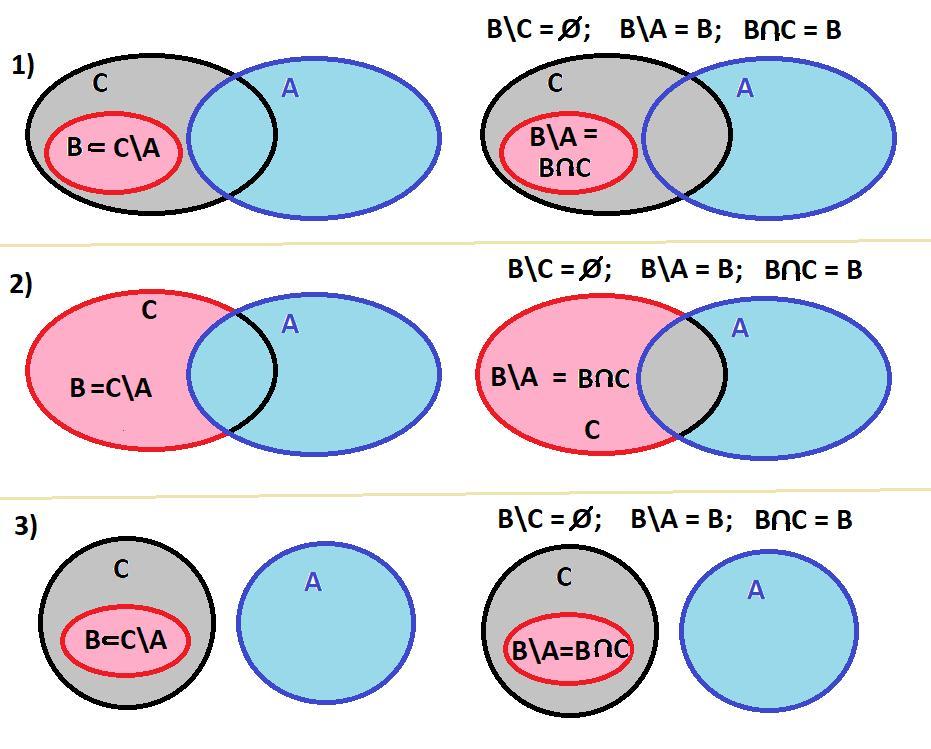
В приложении три схемы
1) B ⊂ C\A , С ∩ А ≠ ∅
множества С и А пересекаются и множество В строго включается в множество C\A.
2) B = C\A , С ∩ А ≠ ∅
множества С и А пересекаются и множество В совпадает с множеством C\A.
3) B ⊂ C\A , С ∩ А = ∅
множества С и А не пересекаются и множество В строго включается в множество C\A = С.
Пояснения :
Так как множество В является подмножеством B ⊆ C\A , то
- B ⊆ C
- B\C = ∅
- множества В и А не пересекаются ⇒ B\А = В
- B∩C = B.
(B\C) ∪ (B\A) = ∅ ∪ B = B = B∩C
Равенство множеств является частым случаем нестрогого включения множеств:
(B\C) ∪ (B\A) ⊆ B∩C
==============================
Возможны другие, аналогичные или более простые варианты отношения множеств, например :
а) B = C, C ∩ A = ∅
б) B = ∅; C = A и т.п