Ответы
Ответ дал:
2
Ответ:
Да.
Объяснение:
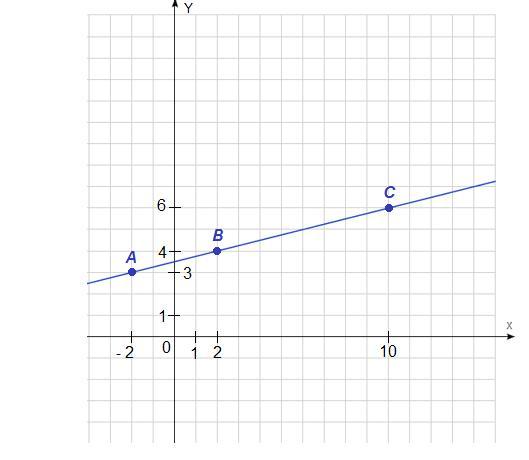
А (- 2; 3), В (2 ; 4), С (10; 6)
Составим уравнение прямой, проходящей через точки А и В.
y = kx+b
Подставим координаты точек в уравнение прямой и решим получившуюся систему уравнений.
Уравнение прямой, проходящей через точки А и В:
y = 0,25x + 3,5
Чтобы узнать, лежит ли точка С на прямой АВ, подставим ее координаты в уравнение прямой:
6 = 0,25 · 10 + 3,5
6 = 2,5 + 3,5
6 = 6 - верно, значит
точка С лежит на прямой АВ.
Точки А, В и С принадлежат одной прямой.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад