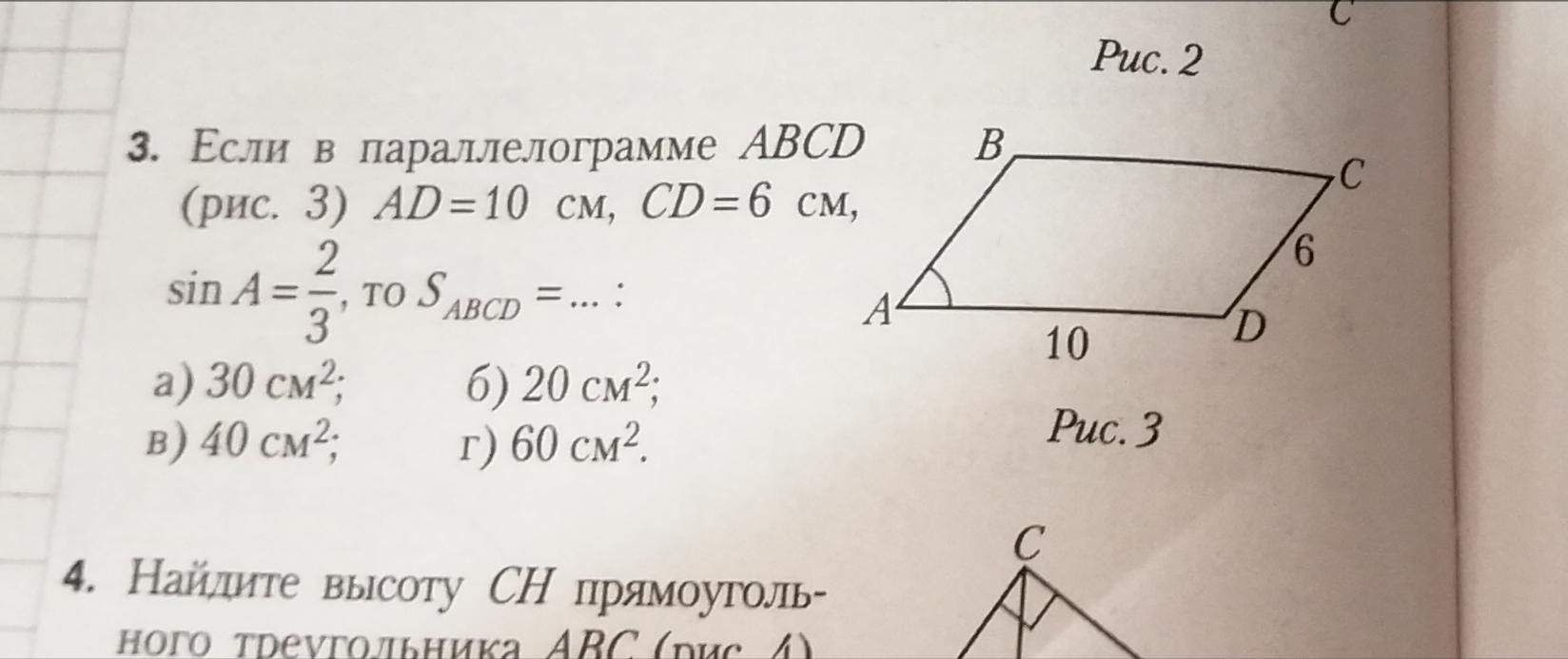
Если в параллелограмме ABCD AD= 10 см CD =6 см синус A2/3 то Sabcd=
A) 30 см ^2
B)20 см^2
Д) 40 см^2
Б) 60см^2
Приложения:
Ответы
Ответ дал:
4
Дано :
Четырёхугольник ABCD - параллелограмм.
AD = 10 см, CD = 6 см, sin(∠A) = .
Найти :
= ?
Решение :
- Площадь параллелограмма равна произведению его двух смежных сторон на синус угла между ними.
Следовательно, = AD*AB*sin(∠A) = 10 см*6 см*
= 40 см² (так как AB = CD = 6 см по свойству параллелограмма).
Ответ :
в) 40 см².
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад