плиз очень срочно
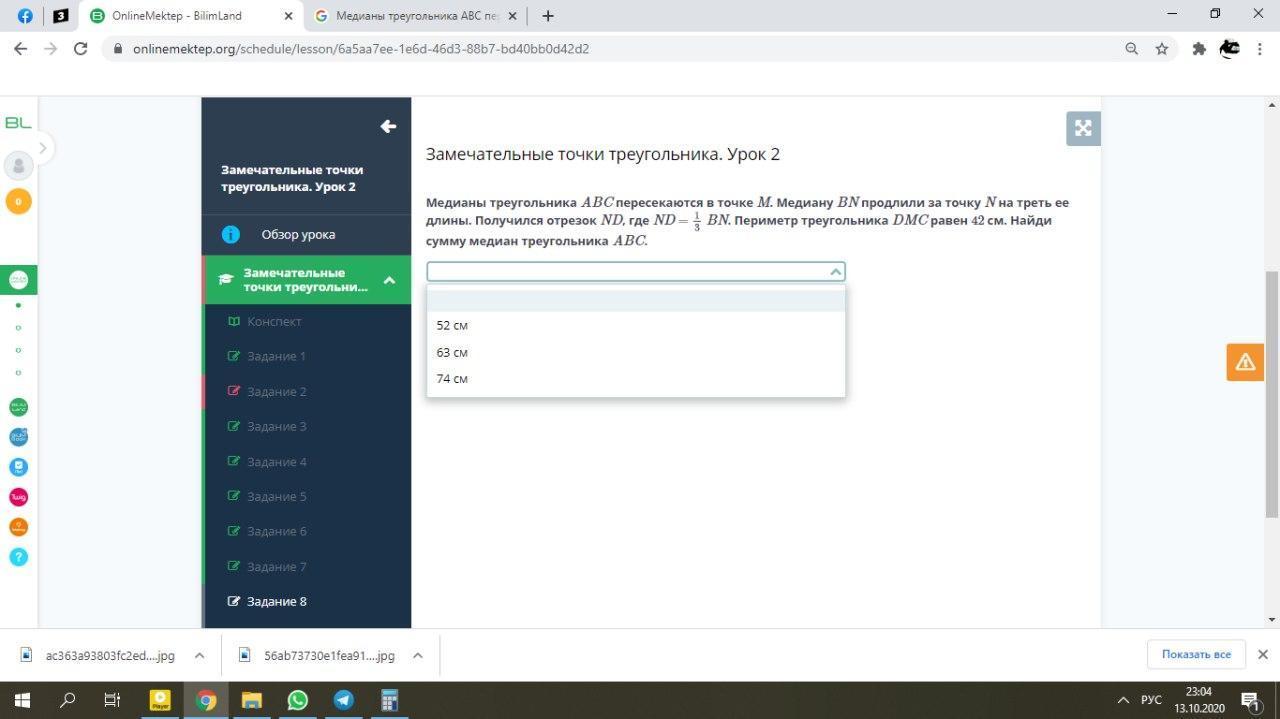
Медианы треугольника ABC пересекаются в точке M. Медиану BN продлили за точку N на треть ее длины. Получился отрезок ND, где ND =
BN. Периметр треугольника DMC равен 42 см. Найди сумму медиан треугольника ABC.
Приложения:
Ответы
Ответ дал:
148
Медианы треугольника точкой пересечения делятся в отношении 2:1 от вершины.
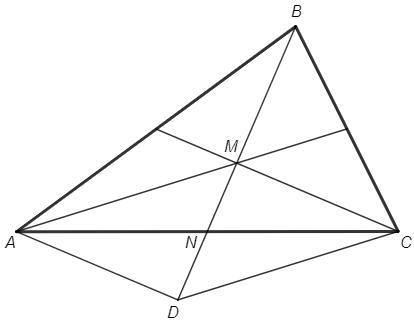
MN =1/3 BN =ND
N - середина AC
Диагонали четырехугольника AMCD точкой пересечения делятся пополам - AMCD параллелограмм, AM=DC.
DC =AM =2/3 m_a, CM =2/3 m_c, DM =2/3 m_b
P(DMC) =2/3 (m_a +m_b +m_c) => m_a +m_b +m_c =42 *3/2 =63 (см)
Приложения:
yasmin2122:
спасибо
Правильно
правильно
спасибо
спасибо:)
спс
Спасибо большое!
спс
дәәәәәәәәәәу рахмет
ой спасибы
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад