в классе 35 учеников каждый из них пользуются одним из видов городского транспорта метро автобуса троллейбуса всеми тремя видами транспорта пользуются 6 учеников метро и автобусом 15 учеников метро и троллейбусом 13 учеников троллейбусом и автобусом 5 учеников Сколько учеников пользоваться только одним видом транспорта
Ответы
Ответ:
только одним видом транспорта пользуются 10 учеников
Пошаговое объяснение:
в условие вкралась ошибка. не могут троллейбусом и автобусом пользоваться 5 учеников, когда всеми тремя уже пользуются 6!
насколько я помню эту задачу (это олимпиадная задачка), там троллейбусом и автобусом пользуются 9 учеников
так и посчитаем
здесь можно и просто считать, но круги Эйлера могут сильно помочь
итак
А - множество тех, кто пользуется автобусом
М - множество тех, кто пользуется метро
Т -множество тех, кто пользуется троллейбусом
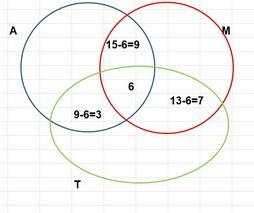
в самом центре у нас пересечение всех трех множеств, т.е. те, кто пользуется всем тремя видами транспорта.
ставим туда цифру 6 (по условию
пересечение А∩М - по условию 15, но 6 мы уже поставили в центр, значит остается 15-6 = 9
пересечение А∩Т - по условию 9, но 6 мы уже поставили в центр, значит остается 9-6 = 3
пересечение Т∩М - по условию 13, но 6 мы уже поставили в центр, значит остается 13-6 = 7
вот, собственно и всё.
теперь нам осталось только сложить все цифры в пересечениях множеств и вычесть это из 35
сразу несколькими видами транспорта пользуются 9+3+6+7=25 уч
только одним видом транспорта пользуются 35-25=10 учеников
ответ
10 учеников