Question

На рисунке RO = 20, ∠OPK = 30°. Вычисли OK.

Answer 1

Ответ:

10

Объяснение:

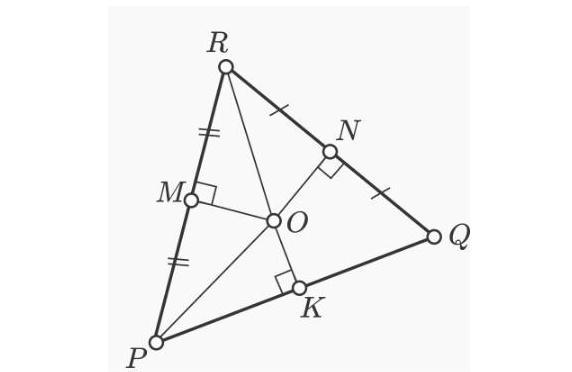
На рисунке О - точка пересечения серединных перпендикуляров ОМ и ON к сторонам PR и RQ треугольника соответственно.

Все точки серединного перпендикуляра к отрезку равноудалены от его концов.

Значит, OP = OR = OQ = 20.

Рассмотрим ΔРОК:

∠РКО = 90°, ∠ОРК = 30°, ОР = 20, значит

ОК = 1/2 ОР = 1/2 · 20 = 10 по свойству катета, лежащего против угла в 30°.