Question

В треугольнике ABC проведены медианы BL и CN, пересекающиеся в точке М. Пусть 2
— середина отрезка BM, а R – середина СМ. Известно, что площадь треугольника QAR
равна 15.
Чему равна площадь треугольника АВС?

Answer 1

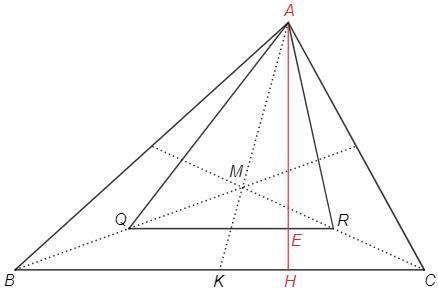
QR - средняя линия в BMC

QR||BC, QR=1/2 BC

Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1 от вершины.

AK - медиана, AM:MK =2:1

По теореме Фалеса QR делит MK в том же отношении, что и MB - пополам. Следовательно QR делит AK в отношении 5:1 и в том же отношении делит AH.

AE =5/6 AH

S(QAR)/S(ABC) =QR*AE/BC*AH =1/2 *5/6 =5/12

S(ABC) =15* 12/5 =36