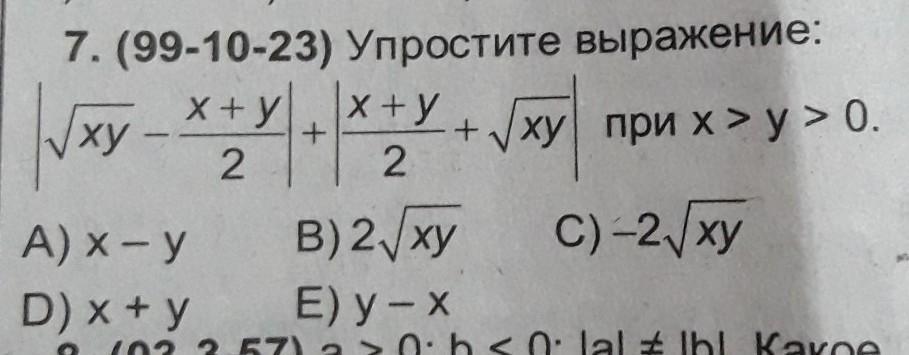Ответы
Ответ дал:
1
Автор задания явно сейчас проходит в школе неравенство Коши между средним арифметическим и средним геометрическим двух положительных чисел. Говорю это с небольшим укором, поскольку, если бы автор немного подумал, он бы сам справился с этой задачей. Ну да ладно.
По неравенству Коши
второй модуль можно отбросить в силу положительности подмодульного выражения, поэтому всё выражение равно x+y.
Ответ: D
нет, этой темы у нас вообще в учебнике нет
Неравенство Коши для двух чисел почти очевидно, так как (x+y)/2-\sqrt{xy}=(\sqrt{x}-\sqrt{y})^2/2>=0
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад