Question

Чему равно ускорение?

Answer 1

Ответ:

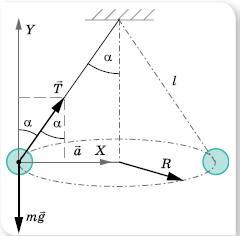
Первый рисунок. Не совсем понятно: если угол известен, то решение простое - с применением тангенса угла и g, но тогда R и l не нужны. Если угол неизвестен, то R и l нужно использовать. Приведу оба варианта.

1)

$F=ma\\OX: |T|*sina=ma_x\\OY:|T|*cosa-mg=ma_y=0 =>|T|*cosa=mg=>|T|=\frac{mg}{cosa} \\OX: \frac{mg}{cosa}*sina=ma_x\\ma = mg\frac{sina}{cosa} \\a = g*tga$

2)

$F=ma\\OX: |T|*sina=ma_x\\OY:|T|*cosa-mg=ma_y=0 =>|T|*cosa=mg=>|T|=\frac{mg}{cosa} \\OX: \frac{mg}{cosa}*sina=ma_x\\sina=\frac{R}{l}=>cosa=\sqrt{1-sin^{2}a}=\sqrt{1-(\frac{R}{l})^{2} }=\sqrt{\frac{l^2-R^2}{l^2}}=\frac{\sqrt{l^2-R^2} }{l}\\ma=\frac{mg}{\frac{\sqrt{l^2-R^2} }{l} } *\frac{R}{l}=\frac{mgl}{\sqrt{l^2-R^2} }*\frac{R}{l}= \frac{mgR}{\sqrt{l^2-R^2} }\\a = \frac{gR}{\sqrt{l^2-R^2} }$

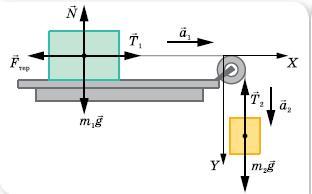
Второй рисунок. Опять же - есть даже три пути: с известным "мю", с известной силой натяжения нити и с известной силой трения:

1)

$F = ma\\T_1=T_2=T\\a_1=a_2=a\\F_m_p = MN\\ OX:-F_m_p+T=m_1a_x\\OY_1: -N+m_1g = m_1a_y=0=>m_1g=N\\OY_2: m_2g-T=m_2a_y\\OX: T-Mm_1g=m_1a_x\\m_1a+m_2a=T-Mm_1g+m_2g-T\\a(m_1+m_2)=m_2g-Mm_1g\\a=\frac{g(m_2-Mm_1)}{m_1+m_2}$.

2)

$F = ma\\T_1=T_2=T\\a_1=a_2=a\\F_m_p = MN\\ OX:-F_m_p+T=m_1a_x\\OY_1: -N+m_1g = m_1a_y=0=>m_1g=N\\OY_2: m_2g-T=m_2a_y\\OX: T-Mm_1g=m_1a_x=>M=\frac{T-m_1a_x}{m_1g}\\m_1a+m_2a=T-Mm_1g+m_2g-T\\a(m_1+m_2)=g(m_2-Mm_1)\\a=\frac{g(m_2-\frac{T-m_1a}{m_1g}*m_1) }{m_1+m_2}= \frac{g(m_2-\frac{T-m_1a}{g}) }{m_1+m_2}=\frac{m_2g-(T-m_1a)}{m_1+m_2}=\frac{m_2g}{m_1+m_2} -\frac{T-m_1a}{m_1+m_2}$

$a+\frac{T-m_1a}{m_1+m_2}=\frac{m_2g}{m_1+m_2}\\\frac{a(m_1+m_2)+T-m_1a}{m_1+m_2}= \frac{m_2g}{m_1+m_2}\\\\a(m_1+m_2-m_1)+T=m_2g\\a*m_2=m_2g-T\\a=\frac{m_2g-T}{m_2}$

3)

$F = ma\\T_1=T_2=T\\a_1=a_2=a\\ OX:-F_m_p+T=m_1a_x\\OY_1: -N+m_1g = m_1a_y=0\\OY_2: m_2g-T=m_2a_y\\m_1a+m_2a=T-F_m_p+m_2g-T\\a(m_1+m_2)=m_2g-F_m_p\\a=\frac{m_2g-F_m_p}{m_1+m_2}$