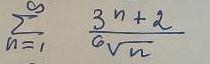Ответы
Ответ дал:
1
Минорантный ряд расходится, значит по признаку сравнения расходится и мажорантный ряд
.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад