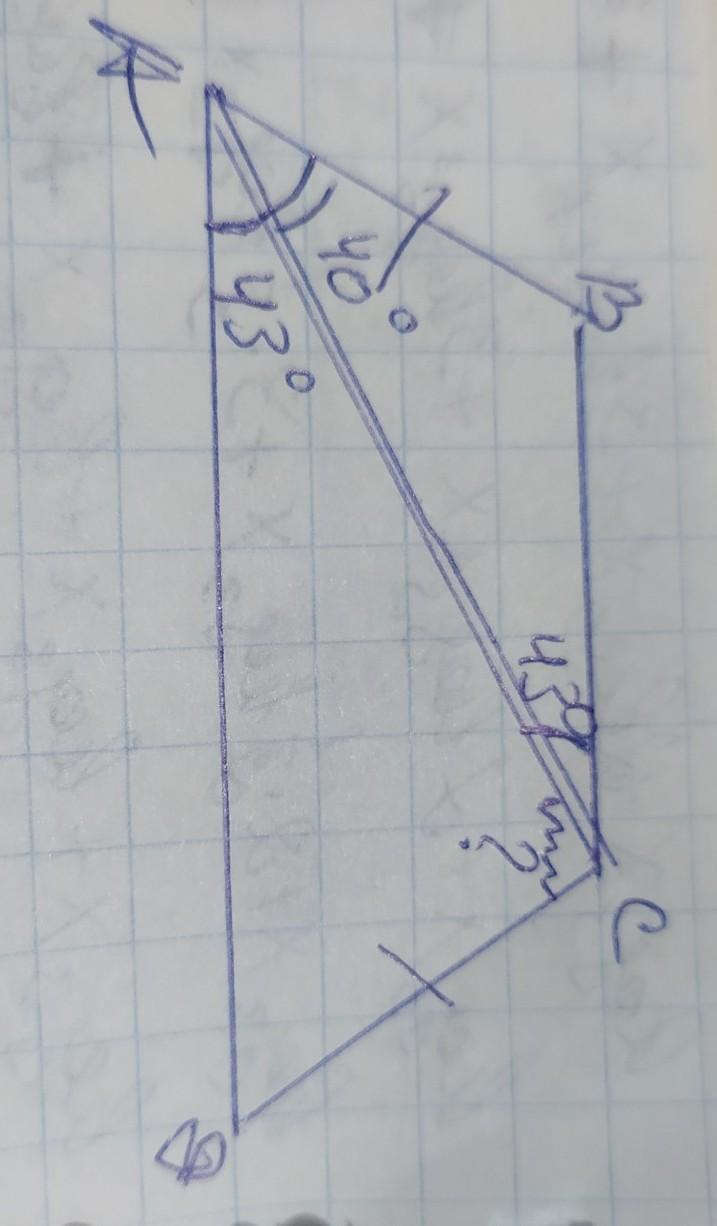
В трапеции ABCD известно, что AB=CD, угол CAD=43 и угол CAB=40. Найдите угол ACD. Ответ дайте в градусах.
Ответы
Ответ дал:
3
Ответ:
<АСД=54°
Объяснение:
если АВ=СД, то трапеция равнобедренная, поэтому <А=<Д и <В=<С. АС - диагональ трапеции, которая делит угол А на 40° и 43°. АС является секущей при параллельных ВС и АД поэтому <САД=<ВСА=43°. Сумма углов трапеции прилегающих к одной боковой стороне составляет 180°, поэтому <В=<С=180–40°–43°=97°. Тогда <АСД=97–43=54°
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад