Найдите все значения параметра a, при которых система уравнений  имеет бесконечное множество решений.
имеет бесконечное множество решений.
Приложения:
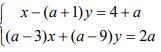
Ответы
Ответ дал:
2
Ответ:
а₁=4
а₂=-3
Пошаговое объяснение:
Условие для того чтоб система имела бесконечное множество решений:
Вычислим определитель и найдём а, при которых он равен 0.
а-9+(а+1)(а-3)=0
а-9+а²+а-3а-3=0
а²-а-12=0 а₁=4 а₂=-3
Подставим а₁=4
При а₁=4 система имеет беск. множество решений
Подставим а₂=-3
При а₂=-3 система имеет беск. множество решений
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
9 лет назад