Question

Сроооччччнннооо!!!!!

Реши неравенство z2−5z+6z2−3z−18>0 .


Ответ запиши в виде числовых промежутков.


Выбери правильный вариант ответа:

(−3;2),(3;6)

(−5;0);(3;+∞)

(−∞;−3),(2;3),(6;+∞)

(−∞;−5);(0;3)

(−∞;−3],(2;3),[6;+∞)

(−∞;−3],[2;3],[6;+∞)

[−3;2];[3;6]

Answer 1

Ответ:

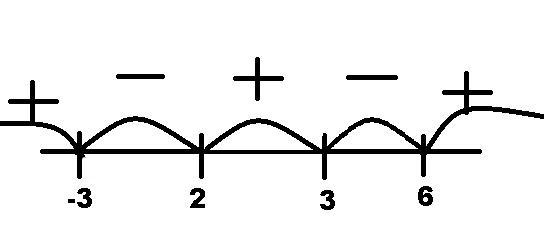
3)  (-∞;-3)∪(2;3)∪(6;+∞)

Объяснение:

$\frac{z^2-5z+6}{z^2-3z-18}>0$

Разложим числитель и знаменатель на множители:

$z^2-5z+6\\D=25-4*6=25-24=1\\z_{1}=\frac{5+1}{2}=3\\ z_{2}=\frac{5-1}{2}=2\\ z^2-5z+6=(z-3)(z-2)$

$z^2-3z-18\\D=9-4*(-18)=9+72=81\\z_{1}=\frac{3+9}{2}=6\\ z_{2}=\frac{3-9}{2}=-3\\z^2-3z-18=(z-6)(z+3)$

$\frac{(z-3)(z-2)}{(z-6)(z+3)} >0$

Нанесём числа, при которых либо числитель, либо знаменатель обнуляется, на числвую прямую.(Все числа выколоты, т.к. строгое неравенство)

С помощью числовой прямой находим решения: (-∞;-3)∪(2;3)∪(6;+∞)