Дан выпуклый четырехугольник ABCD площади S и точка M внутри его. Точки P, Q, R, S симметричны точке M относительно середин сторон четырехугольника ABCD. Найти площадь четырехугольника PQRS
Ответы
Ответ дал:
2
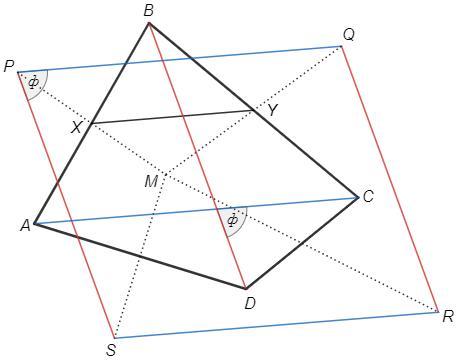
X - середина AB, Y - середина BC
Симметрия относительно точки: X - середина MP, Y - середина MQ
XY - средняя линия △PMQ и △ABC => PQ||XY||AC, PQ=2XY=AC
Аналогично SR||AC, SR=AC, PS||BD||QR, PS=BD=QR
Таким образом PQRS - параллелограмм и его стороны параллельны диагоналям ABCD - значит угол (ф) между сторонами PQRS равен углу между диагоналями ABCD.
S(ABCD) =1/2 AC*BD*sinф =S
S(PQRS) =PQ*PS*sinф =AC*BD*sinф =2S
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад