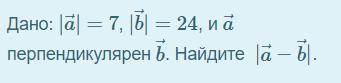Ответы
Ответ дал:
1
Ответ:
25
Пошаговое объяснение:
Общая формула для модуля разности векторов:
Т.к. вектора перпендикулярны, то:
Тогда:
Замечание:
Можно было сразу сказать, что вектора являются катетами в прямоугольном треугольнике, и воспользоваться теоремой Пифагора
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад