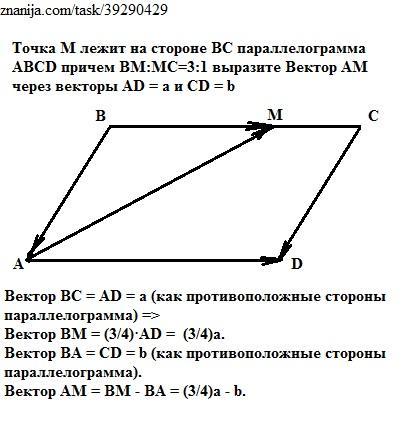
точка М лежит на стороне BC параллелограмма ABCD причем BM:MC=3:1 выразите Вектор AM через векторы AD равно a и CD равно b

Ответы

Ответ дал: Andr1806

Ответ:

Вектор АМ = (3/4)а - b.

Объяснение:

Вектор ВС = AD = а (как противоположные стороны параллелограмма).

Вектор ВМ = (3/4)·AD = (3/4)а.

Вектор ВА = CD = b (как противоположные стороны параллелограмма).

Вектор АM = ВM - ВА = (3/4)а - b. (по правилу вычитания векторов).

Приложения:

timofejcen33: спасибо,но иы опаздал

sarvinoz100718: пасибо

armybtsomarov: а как получается 3/4?

Аноним: Точка М лежит на стороне ВС параллелограмма АВСD, причем ВМ:МС = 3:1. Выразите вектор АМ через векторы ВС=a и ВА=b

Помогите пожалуйста с этим

armybtsomarov: есть Вк?

armybtsomarov: или инст?

Аноним: да

Аноним: а здесь не можете?

armybtsomarov: нет

Andr1806: Так как отношение частей отрезка 3:1, то отношение этих частей ко всему отрезку равно 3:4 и 1:4. (Отрезок равен сумме его частей).

Вас заинтересует

Английский язык

1 год назад

ПОМОГИТЕ, ПРОШУ ДАЮ 20 Б!!

Математика

1 год назад