Ответы
Ответ дал:
0
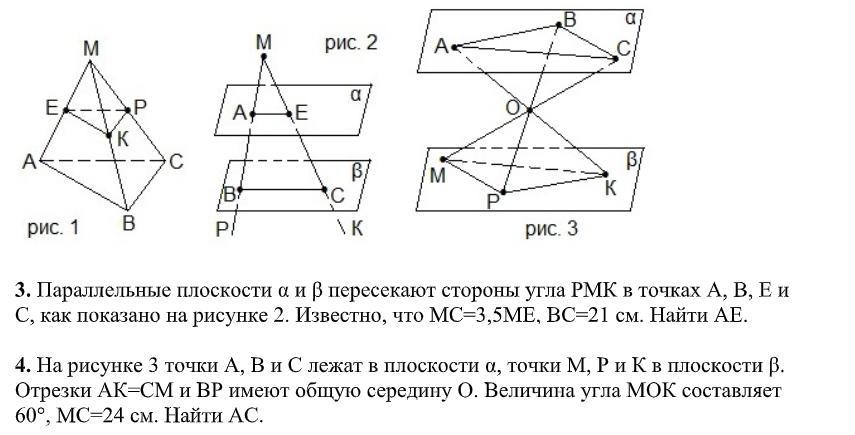
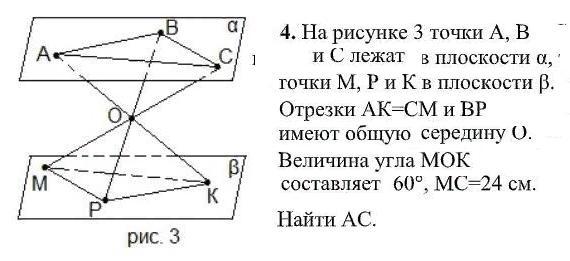
Точки А,В и С лежат в плоскости α, точки М, Р и К в плоскости β. Отрезки АК=СМ и ВР имеют общую середину О. Величина угла МОК составляет 60°, МС=24 см. Найти АС.
Объяснение:
1) О-середина АК , значит АО=ОК.
О-середина СМ, значит МО=ОС.
Т.к. АК=СМ , то тАО=ОК=МО=ОС=12 см.
2)МС∩АК=О ,поэтому эти две пересекающиеся прямые определяют плоскость (АСК) единственным образом. В Этой плоскости лежат треугольники АОС и КОМ..
3)ΔАОС =ΔКОМ по 2 сторонам и углу между ними :АО=ОК, СО=ОМ , см п1, ∠АОС=∠КОМ как вертикальные.В равных треугольниках соответственные элементы равны⇒ ∠АОС=60°
4) ΔАОС , по т. косинусов АС²=АО²+ОС²-2*АО*ОС*cos 60° ,
AC²=144+144-2*1444*(1/2)
AC=12 см.
Приложения:
selfcare39:
Здравствуйте, помогите пожалуйста с геометрией! ДАЮ 70 БАЛЛОВ! Отмечу 5 звёзд и сделаю лучший ответ! Всего 3 задания.
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад