Question

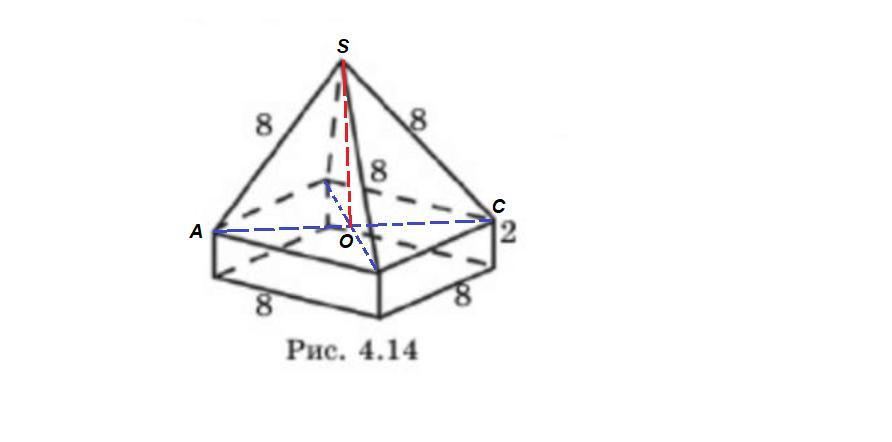
Найдите объем составного тела, в нижней части которого расположен прямой параллелипипед размером 8х8х2, а в верхней части - правильная четырехугольная пирамида.
Задание 4.5

Answer 1

Ответ:

$V=\dfrac{128(3+2\sqrt{2})}{3}$

Объяснение:

Пирамида правильная, значит в основании лежит квадрат.

Значит, и основания прямого параллелепипеда - квадраты.

Объем прямоугольного параллелепипеда равен произведению трех его измерений:

V₁ = 8 · 8 · 2 = 128

В правильной пирамиде высота проецируется в центр основания - точку О.

АС = 8√2 как диагональ квадрата.

АО = АС/2 = 4√2 (диагонали квадрата точкой пересечения делятся пополам)

Из прямоугольного треугольника SAO по теореме Пифагора найдем высоту пирамиды:

SO = √(SA² - AO²) = √(64 - 32) = √32 = 4√2

Объем пирамиды:

V₂ = 1/3 Sосн. · SO = 1/3 · 8² · 4√2 = 256√2/3

Объем тела:

$V=V_1+V_2=128+\dfrac{256\sqrt{2}}{3}=\dfrac{128(3+2\sqrt{2})}{3}$