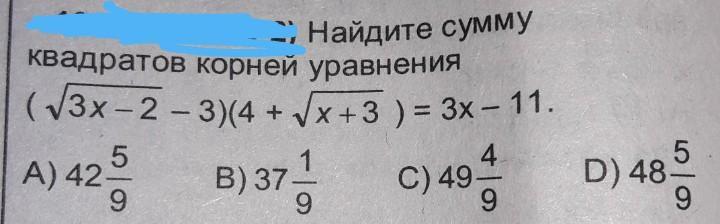Question

помогите пожалуйста​

Answer 1

$(\sqrt{3x-2}-3)(4+\sqrt{x+3})=3x-11$  ОДЗ: $x\ge \frac{2}{3}.$

Замечаем, что $(\sqrt{3x-2}-3)(\sqrt{3x-2}+3)=3x-11,$ поэтому можно переписать уравнение в виде

$(\sqrt{3x-2}-3)(4+\sqrt{x+3})=(\sqrt{3x-2}-3)(\sqrt{3x-2}+3).$

Видим, что если $\sqrt{3x-2}-3=0,$ то уравнение превращается в равенство 0=0. Отсюда первый корень уравнения $x=\frac{11}{3}\in$ ОДЗ.

Далее можно сократить на эту общую скобку левой и правой части:

$4+\sqrt{x+3}=\sqrt{3x-2}+3;\ \sqrt{3x-2}-\sqrt{x+3}=1.$

Такое уравнение можно решать миллионом разных способов, автор задания, несомненно, знает как минимум тысячу из них. Применим 1001-й способ, который  скорее всего не входит в тысячу самых популярных и который я обычно называю методом метаморфоз. Обозначим

$\sqrt{3x-2}=a\ge 0;\ \sqrt{x+3}=b\ge 0.$

Заметим, что $3x-2=a^2;\ x+3=b^2\Rightarrow 3b^2-a^2=11.$

Получаем систему

$\left \{ {{a-b=1} \atop {3b^2-a^2=11}} \right. \Leftrightarrow \left \{ {{a=b+1} \atop {3b^2-(b+1)^2=11}} \right. .$

Решим второе уравнение:

$2b^2-2b-12=0;\ (b-3)(b+2)=0;$ но поскольку $b\ge 0\Rightarrow b=3;\ x=6.$

Подставляя его в уравнений (которое мы решаем 1001-м способом), получаем верное равенство 4-3=1.

Возведя найденные корни исходного уравнения в квадрат и сложив их, получаем

Ответ: C

Замечание: я не понимаю, какие умения проверяются возведением в квадрат полученных чисел и их складыванием. Гуманнее было бы попросить, скажем, перемножить их.

Замечание. А сама задача превосходная.