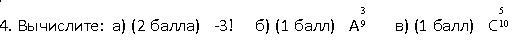Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
1) -3! = -6
2) A(9,3) = 9!/6! = 9*8*7 = 504
3) C(10,5) = 10!/(5!*5!) = 252
sdawda123:
Спасибо,а после равно в строчку идёт?
или деление только в 2?
Не понял вопроса
Ответ дал:
2
Ответ:
Пошаговое объяснение:
1)
Выражение n! - это факториал числа. Он равен
Вычислим для n = 3
2) - число размещений из m по n. Оно равно
Для нашего случая
3) - число сочетаний из n по k. Оно равно
Для нашего случая
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад