Question

Изобразить на комплексной плоскости множество точек z удовольтворяющих условию |z - i|+|z + i| = 2​

Answer 1

Пусть $\Re z=x, \Im z=y$

$|x+i(y-1)|+|x+i(y+1)|=2\\ \sqrt{x^2+(y-1)^2}+\sqrt{x^2+(y+1)^2}=2\\ x^2+(y-1)^2+x^2+(y+1)^2+2\sqrt{x^2+(y-1)^2}\sqrt{x^2+(y+1)^2}=4\\ 2x^2+2y^2+2\sqrt{x^4+x^2(2y^2+2)+(y^2-1)^2}=2\\ \sqrt{(x^2+(y^2-1))^2+4x^2}=-(x^2+(y^2-1))\Rightarrow -(x^2+(y^2-1))\geq 0\;\;(1)$

Возводя в квадрат, получим:

$(x^2+(y^2-1))^2+4x^2=(x^2+(y^2-1))^2\\ 4x^2=0\Rightarrow x=0$

Подставляя $x=0$ в $(1)$, получим: $y^2-1\leq 0\Rightarrow |y|\leq 1\;\;\;(2)$

Подставляя $x=0$ в исходное уравнение, получим

$\sqrt{(y-1)^2}+\sqrt{(y+1)^2}=2\\ |y-1|+|y+1|=2$

Тогда, с учетом $(2)$, получаем $1-y+y+1=2\Rightarrow 2=2$ - верное равенство.

А значит мн-во точек с координатами $(0,y), |y|\leq 1$ удовлетворяют уравнению.

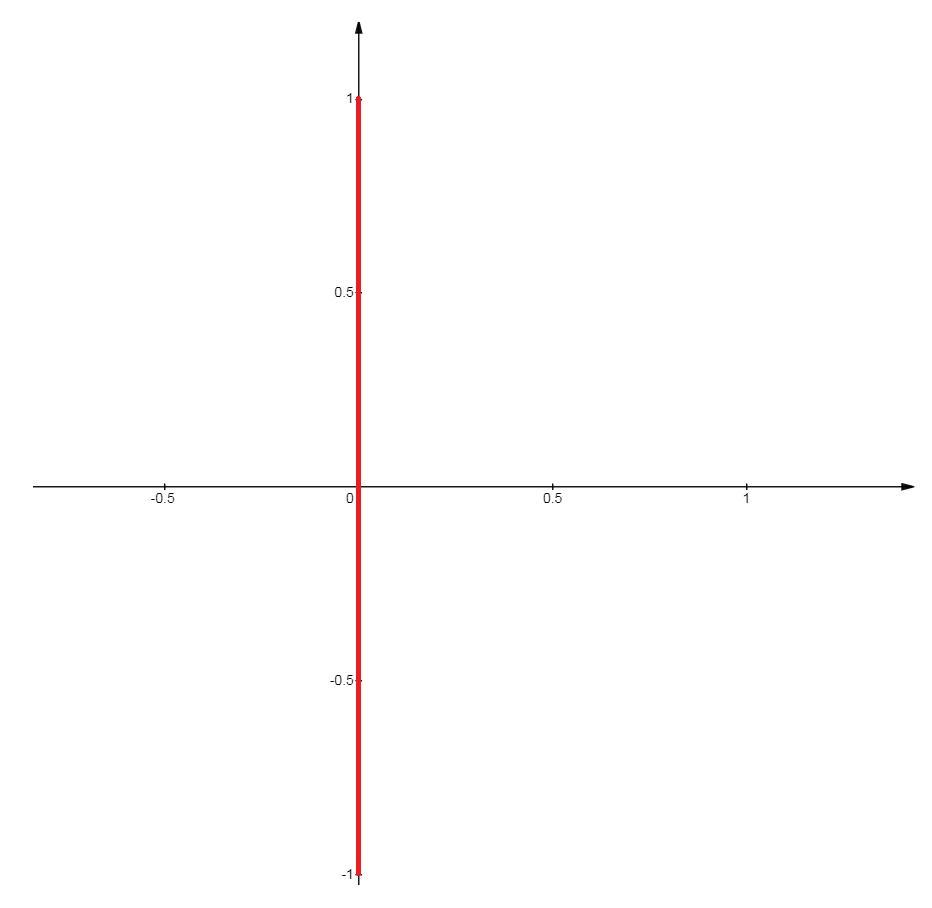
Тогда мн-во точек, удовлетворяющих условию |z - i|+|z + i| = 2​, имеет вид $\{z\in C | \Re z=0,-1\leq \Im z\leq 1\}$ - отрезок, соединяющий точки $(0;-1),(0;1)$