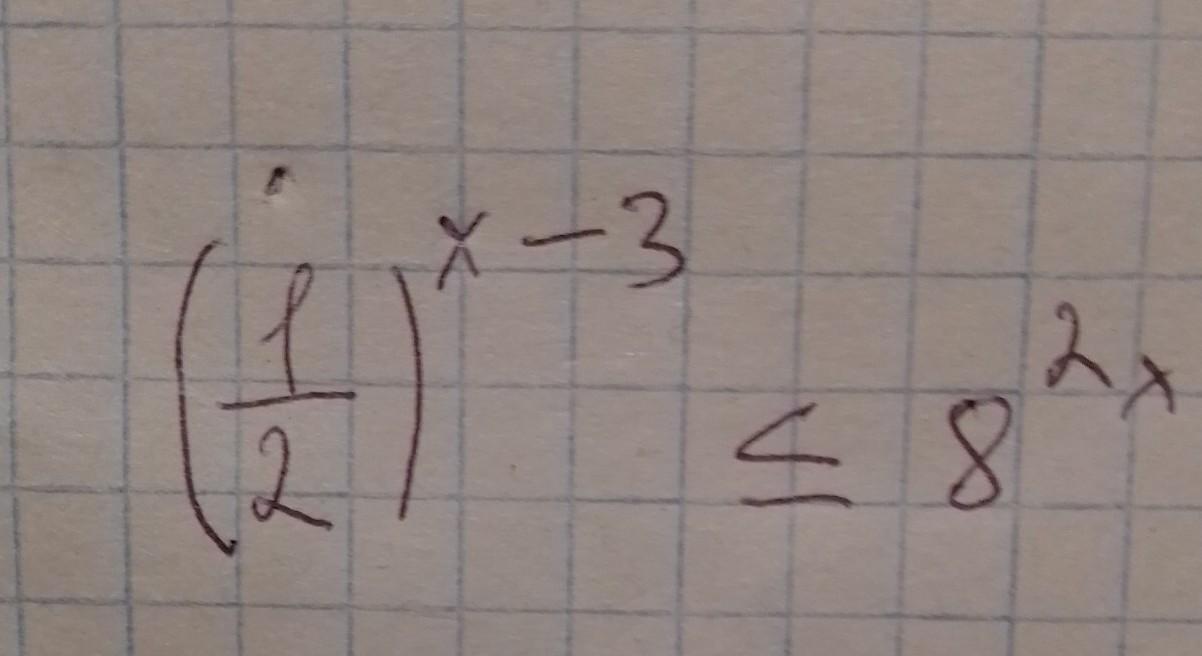Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
по свойствам степени преобразуем левую и правую части неравенства в степень с основанием а=2.
1).
2).
3).
простейшее показательное неравенство, основание степени а=2, 2>1, знак неравенства не меняем
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад