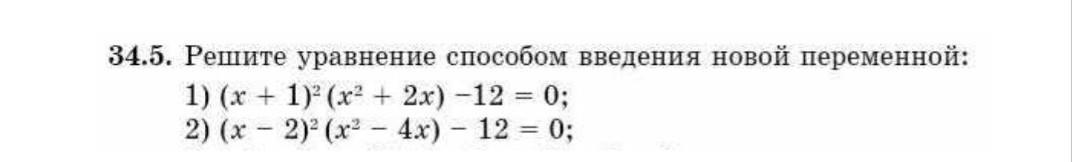Ответы
Ответ дал:
1
Ответ:
1)
2)
Пошаговое объяснение:
1)
Вынесем во второй скобке x за скобку:
Обозначим x + 1 = t, ⇒ x = t - 1
Мы получили биквадратное уравнение относительно переменной t.
Обозначим t = a;
По т.Виета:
решений нет
2) Решаем аналогично.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад