Медианы прямоугольного
треугольника ABC (AB-
гипотенуза) пересекаются в
точке М. Найти гипотенузу АВ,
если CM равно 6 см.
Ответы
Ответ дал:
6
Дано :
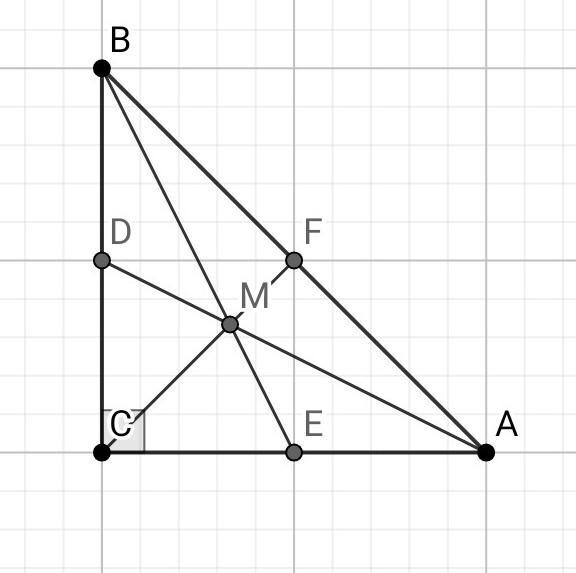
∆АВС - прямоугольный (∠С = 90°).
ВЕ, AD, CF - медианы треугольника.
Точка М - точка пересечения медиан.
Найти :
AB = ?
Решение :
- Точка пересечения медиан делит медиану треугольника в отношении 2 : 1, считая от вершины треугольника.
Следовательно, СМ : MF = 2 : 1.
6 см : MF = 2 : 1
MF = 3 см.
Тогда CF = CM + MF = 6 см + 3 см = 9 см.
- Медиана прямоугольного треугольника, проведённая к гипотенузе, равна её половине.
Отсюда AB = 2*CF = 2*9 см = 18 см.
Ответ :
18 см.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад