Question

Помогите плиз

Answer 1

Найдём точки пересечения графиков функции без построения графиков:

1)

$y=\frac{12}{x};y=3x\\\frac{12}{x}=3x\\3x^2=12\\x^2=4\\x_1=2;y_1=3x_1=6\\x_2=-2;y_2=3x_2=-6.$

2)

$y=-\frac{8}{x};y=-2x\\-\frac{8}{x}=-2x\\\frac{8}{x}=2x\\2x^2=8\\x^2=4\\x_1=2;y_1=-2*x_1=-4\\x_2=-2;y_2=-2*x_2=4.$

3)

$y=\frac{2}{x};y=x-1\\\frac{2}{x}=x-1\\\frac{2}{x}*x=(x-1)*x\\2=x(x-1)\\2=x^2-x\\x^2-x-2=0\\x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\a = 1,b=-1;c=-2\\x_1=\frac{1+\sqrt{1-4*1*-2}}{2*1}=\frac{1+\sqrt{9}}{2}=\frac{1+3}{2}=\frac{4}{2}=2\\y_1=x_1-1=2-1=1.\\x_2=\frac{1-\sqrt{1-4*1*-2}}{2*1}=\frac{1-3}{2}=\frac{-2}{2}=-1\\y_2=x_2-1=-1-1=-2.$

4)

$y=\frac{6}{x+1};y=x+2\\\frac{6}{x+1}=x+2\\6=(x+2)(x+1)\\6=x^2+2x+1x+2\\x^2+3x-4=0\\x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\\a = 1;b=3;c=-4\\x_1=\frac{-3+\sqrt{3*3-4*1*-4}}{2*1}=\frac{-3+\sqrt{9+16}}{2}=\frac{-3+\sqrt{25}}{2}=\frac{-3+5}{2}=\frac{2}{2}=1\\y_1=x_1+2=1+2=3.\\x_2=\frac{-3-\sqrt{3*3-4*1*-4}}{2*1}=\frac{-3-5}{2}=\frac{-8}{2}=-4\\y_2=x_2+2=-4+2=-2.$

Найдём точки пересечения графиков функций, построив графики:

1)

$y=\frac{3}{x};y=x+1$

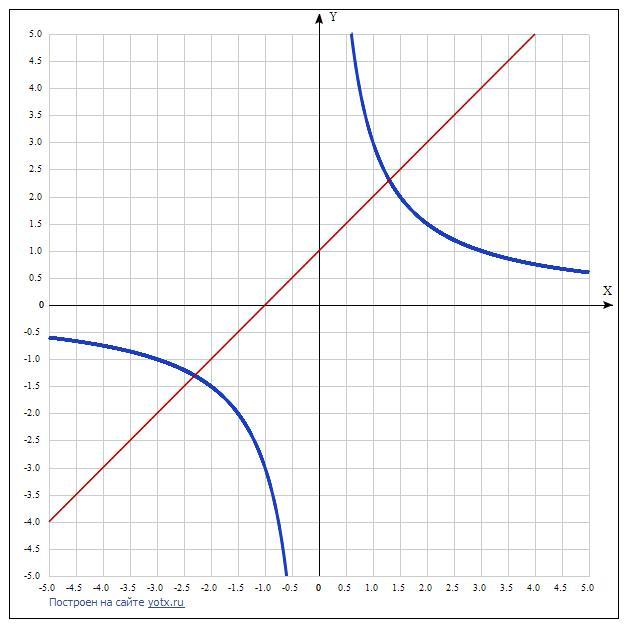
Файл 1-3dividex-x+1.png

2 точки пересечения

2)

$y=-\frac{3}{x};y=1-x$

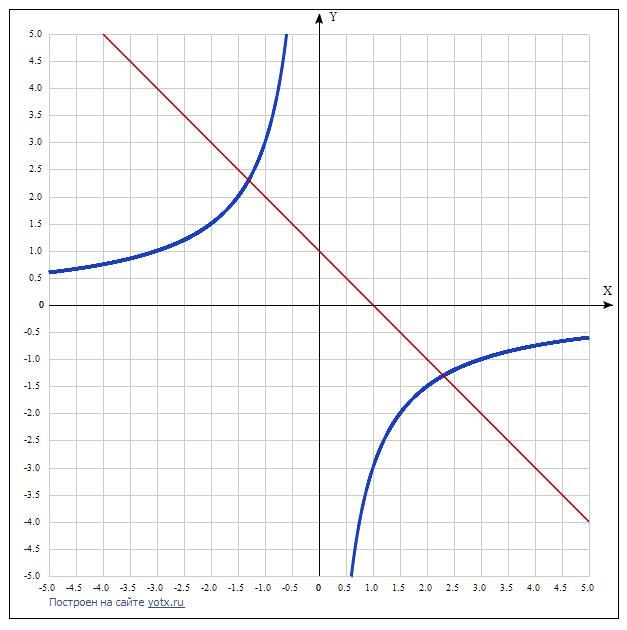
2 точки пересечения

Файл 2-minus3dividex-1-x.png

3)

$y=\frac{2}{x};y=x^2+2$

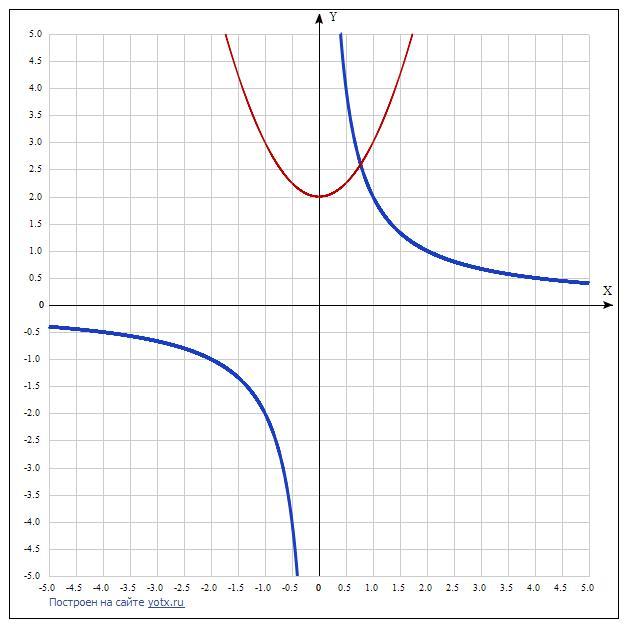
1 точка пересечения

Файл 3-2dividex-x2+2.png

4)

$y=\frac{1}{x};y=x^2+4x$

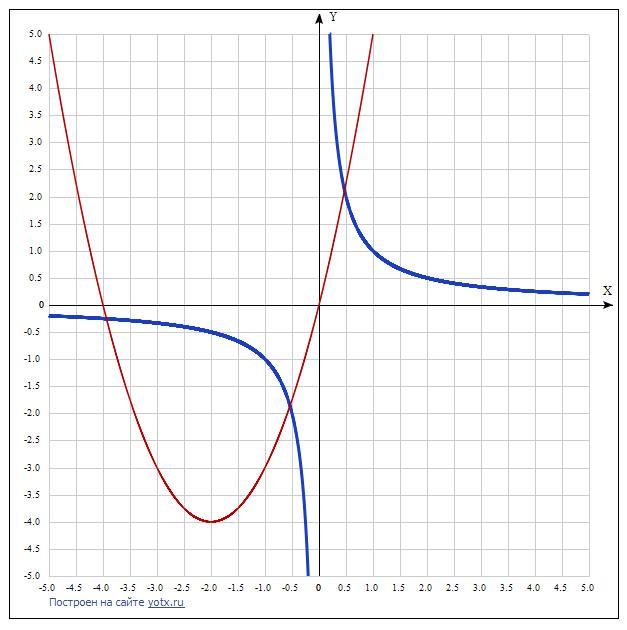
3 точки пересечения

Файл 4-1dividex-x2+4x.png

Объяснение:

Мы можем построить графики функций и посмотреть координаты точек, где пересекаются их линии.

Для нахождения точек пересечения графиков функций без их построения, можно приравнять их части для одной из координат друг другу. Таким образом можно найти, при каких значениях x значения y равны друг другу. А исходя из самих функций, можно потом определить эти самые значения y из значений x.

В итоге получаем координаты x и y для точек пересечения графиков.