Ответы
Задание 1
a) Сумма углов 4угольника 360° => складываем все углы 115° + 72° + 38° + 150° = 375° => 4угольник существовать не может.
b) Формула суммы углов многоугольника - (n-2) × 180°, где n - это кол-во углов. Так как мы знаем сумму, нужно сделать обратную последовательность: 900° ÷ 180° + 2 = 5 + 2 = 7 у многоугольника 7 углов => сторон тоже 7
Задание 2
(Прошу прощения, я без чертежа) Обозначим треугольник ABC среднюю линию - KL => средняя линия отсечёт трапецию AKLC. Меньшее основание трапеции 11 см, оно является средней линией, а сред.линия это 1/2 от основания треугольника т.е. половина. Умножим 11 на 2 = 22 см это большее основание трапеции и основание треугольника то есть 22 см это AC. Средняя линия соединяет середины сторон ABC. Следовательно умножаем каждую боковую сторону на 2. 7×2=14 см это AB, 10×2=20см это BC. Теперь сложим все стороны 14+20+22 = 56 см - P треугольника ABC.
Задание 3 (второе фото)
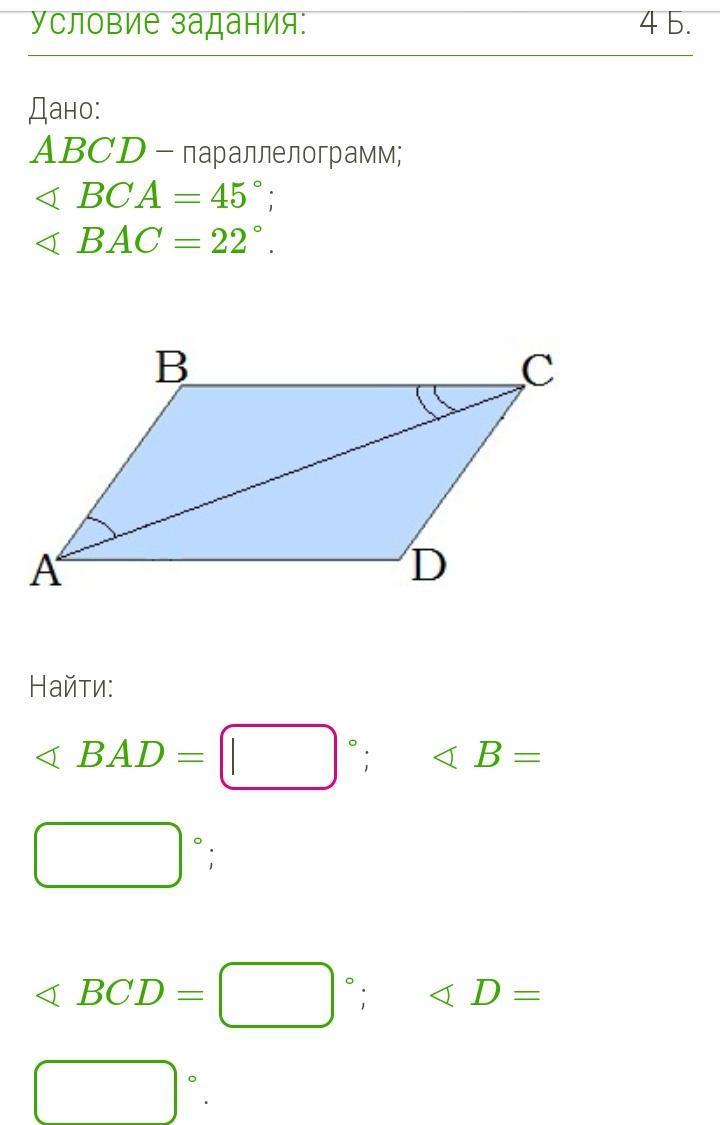
Начнём с того что в параллелограмме диагональ AC это секущая. Значит накрест лежащие углы равны => Угол BCA = CDA = 45°, угол BAC = DCA = 22°
Отсюда узнаём углы BCD и BAD = 45° + 22° = 67° т.к. противолежащие углы параллелограмма равны. Сумма углов к одной стороне равна 180° => угол B = 180° -67°=113° => угол D тоже равен 113° так как противолежащий
Ответ: BAD=67°, B=113°, BCD=67°, D=113°.
Задание 4 (третье фото)
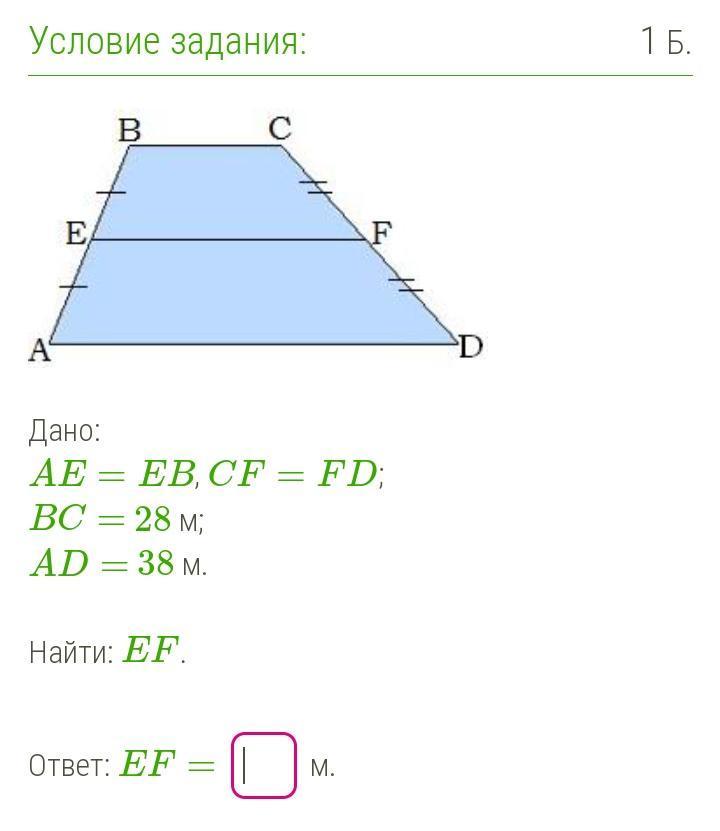
Т.к. EF делит AB и CD пополам и параллельна основаниям - это сред.линия трапеции.
Сред.линия трапеции равна полусумме двух оснований т.е. складываем оба основания и делим на 2.
BC + AD = 28 + 38 = 66 м - это сумма оснований
66 ÷ 2 = 33 м - EF
Ответ: EF = 33 м
Удачи!!!