Даны точки A(8;6) и B(8;12).
Найди координаты точек C и D, если известно, что точка B — середина отрезка AC, а точка D — середина отрезка BC.
C=( )
D=( )
Ответы
Ответ дал:
3
Ответ:
Объяснение:
По формуле координат середины отрезка для точки B и отрезка AC:
По формуле координат середины отрезка для точки D и отрезка BC:
Приложения:

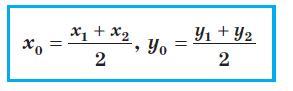
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад