Ответы
Ответ дал:
0
сумма всех натуральных чисел от 7 до 65 это сумма арифмитической прогрессии с первым членом a[1]=7, последним членом a[n]=65 и разницей арифмиттиеческой прогрессии d=1
по формуле общего члена найдем количевство членов
a[n]=a[1]+(n-1)*d
65=7+(n-1)*1
58=n-1
n=58+1=59
по формуле суммы
S=(a[1]+a[n])/2* n
S=(7+65)/2 *59=2 124
по формуле общего члена найдем количевство членов
a[n]=a[1]+(n-1)*d
65=7+(n-1)*1
58=n-1
n=58+1=59
по формуле суммы
S=(a[1]+a[n])/2* n
S=(7+65)/2 *59=2 124
Ответ дал:
0
""""""""""""""""""""""""""""""""""
Приложения:
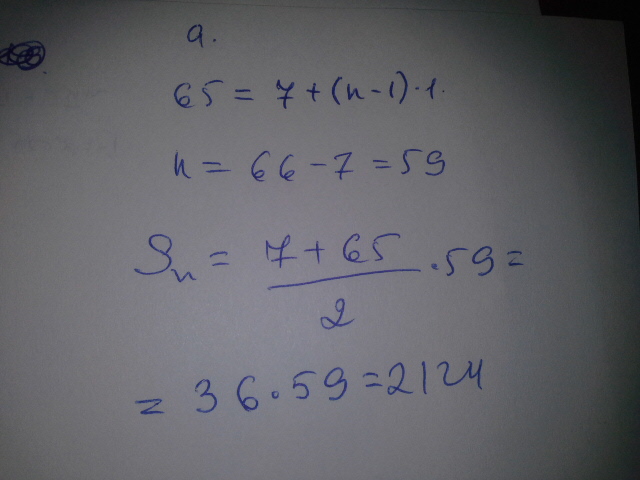
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад