Question

Найдите стороны параллелограмма, если его периметр равен 60 см, а одна из сторон в 4 раза больше другой

Answer 1

Дано :

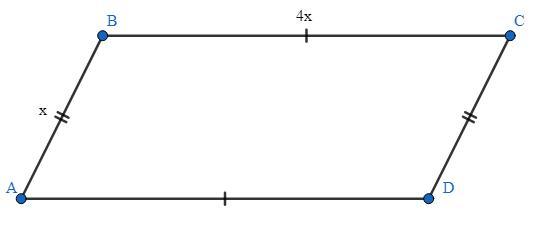
Четырёхугольник ABCD - параллелограмм.

$P_{ABCD}=$ 60 см.

ВС = 4АВ.

Найти :

АВ = ?, ВС = ?, CD = ?, AD = ?

Решение :

Пусть ВС = х, тогда АВ = 4х.

• Периметр параллелограмма равен удвоенной сумме его смежных сторон.

Следовательно, $P_{ABCD} = 2(AB+BC)$

60 см = 2(х + 4х)

30 см = 5х

х = 6 см.

АВ = х = 6 см

ВС = 4х = 4*6 см = 24 см.

• Противоположные стороны равны.

Следовательно, АВ = CD = 6 см, ВС = AD = 24 см.

Ответ :

6 см, 24 см, 6 см, 24 см.