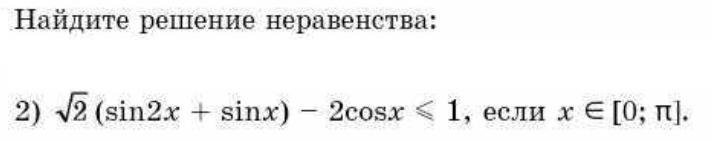Question

Решите неравенство ...............................

Answer 1

Ответ:

x ∈ [0; П/4] U [2П/3; 3П/4]

Объяснение:

√2(sin 2x + sin x) - 2cos x ≤ 1; если x ∈ [0; П]

√2(2sin x*cos x + sin x) - 2cos x - 1 ≤ 0

√2sin x*(2cos x + 1) - (2cos x + 1) ≤ 0

(2cos x + 1)(√2sin x - 1) ≤ 0

Так как произведение ≤ 0, то сомножители имеют разные знаки.

Возможно два варианта:

1)

{ 2cos x + 1 ≤ 0

{ √2sin x - 1 ≥ 0

{ x ∈ [0; П]

Преобразуем

{ cos x ≤ -1/2

{ sin x ≥ 1/√2

{ x ∈ [0; П]

Получаем:

{ x ∈ [2П/3+2Пk; 4П/3+2Пk]

{ x ∈ [П/4+2Пk; 3П/4+2Пk]

{ x ∈ [0; П]

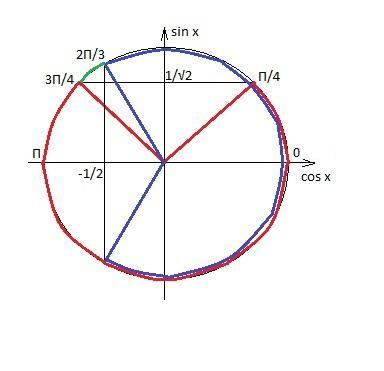
x ∈ [2П/3; 3П/4] (на рисунке показан зеленым цветом)

2)

{ 2cos x + 1 ≥ 0

{ √2sin x - 1 ≤ 0

{ x ∈ [0; П]

Преобразуем

{ cos x ≥ -1/2

{ sin x ≤ 1/√2

{ x ∈ [0; П]

Получаем:

{ x ∈ [-2П/3+2Пk; 2П/3+2Пk]

{ x ∈ [-5П/4+2Пk; П/4+2Пk]

{ x ∈ [0; П]

x ∈ [0; П/4] (на рисунке показан двойным цветом - синим и красным)