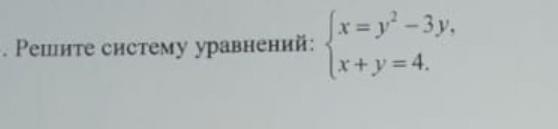Предмет: Алгебра
Автор: selfcare39
Вопрос задан 3 года назад

ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО! РЕШИТЕ полностью!

Приложения:

Ответы

Ответ дал: sangers1959

Объяснение: $\left \{ {{x=y^2-3y} \atop {x+y=4}} \right. \ \ \ \ \left \{ {{4-y=y^2-3y} \atop {x=4-y}} \right. \ \ \ \ \left \{ {{y^2-2y-4=0} \atop {x=4-y}} \right. \ \ \ \ \left \{ {D=20\ \ \ \ \sqrt{D}=2\sqrt{5} } \atop {x=4-y}} \right. \ \ \ \ \left \{ {{y_1=1-\sqrt{5}\ \ y_2=1+\sqrt{5} } \atop {x_1=3+\sqrt{5}\ \ x_2=3-\sqrt{5} }} \right. .$ Ответ: (3+√5;1-√5), (3-√5;1+√5).

selfcare39: у меня ответ вот так выходит \{ {{x=y^2-3y} \atop {x+y=4}} . \ \ \ \ \{ {{4-y=y^2-3y} \atop {x=4-y}} . \ \ \ \ \{ {{y^2-2y-4=0} \atop {x=4-y}} . \ \ \ \ \{ {D=20\ \ \ \ \sqrt{D}=2\sqrt{5} } \atop {x=4-y}} . \ \ \ \ \{ {{y_1=1-\sqrt{5}\ \ y_2=1+\sqrt{5} } \atop {x_1=3+\sqrt{5}\ \ x_2=3-\sqrt{5} }}

selfcare39: не понятно

sangers1959: Это на телефоне?

selfcare39: да

sangers1959: Попробуйте это решение посмотреть на другом телефоне. У меня на компьютере всё видно правильно.

selfcare39: сейчас попробую

karinakadyrova10: у меня тож решение так показано. \{ {{x=y^2-3y} \atop {x+y=4}} . \ \ \ \ \{ {{4-y=y^2-3y} \atop {x=4-y}} . \ \ \ \ \{ {{y^2-2y-4=0} \atop {x=4-y}} . \ \ \ \ \{ {D=20\ \ \ \ \sqrt{D}=2\sqrt{5} } \atop {x=4-y}} . \ \ \ \ \{ {{y_1=1-\sqrt{5}\ \ y_2=1+\sqrt{5} } \atop {x_1=3+\sqrt{5}\ \ x_2=3-\sqrt{5} }} . .

Вас заинтересует

Информатика

2 года назад

Задача C1. Комната ярости (2 балла) Гертруда имеет n тарелок. И хочет разбить их все. По одной. Но тарелки бьются очень звонко. Она опасается, что повредит слух. Известно, что сила звона первой

Русский язык

2 года назад

Расскажите о своих планах на ближайшее будущее в 5-6 предложениях с составным глагольным сказуемым.

Русский язык

2 года назад

В каждом предложение добавить причастный оборот. Изумительный по красоте мир ледников. Снежные поля и ледяные массы покрывают склоны хребтов и вершин и ослепительно сверкают под лучами солнца.

Русский язык

2 года назад