Вычислить границы функций
Приложения:
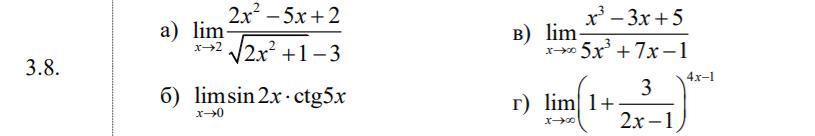
Аноним:
Не помню.
А эту тему? https://znanija.com/task/39656539
Или же эту? https://znanija.com/task/39656294
Нет не смогу, извините.
Ответы
Ответ дал:
1
Задание 1.
Воспользуемся правилом Лопиталя:
Задание 2.
Применим эквивалентности бесконечно малых величин:
Задание 3.
Вынесем общий множитель x³ и отбросим величины, стремящиеся к 0:
Задание 4.
Приведем предел к виду второго замечательного предела
домножил обоих на (корень+3).Знам=2х^2+1-9=2(x-2)(x+2). сократил х-2, подставил в дробь "2", =>1.5*6/8=9/8. mishsvyat
mishsvyat, что не так ? где ошибся, никак не найду
третий пошел сразу
@justDavid, такой ход решения рассмотрен во втором ответе. У Вас возможно 2 в числителе потерялась
Пожалуйста помогите https://znanija.com/task/39686596
mishsvyat, благодарю
в каком это классе?
блин я 6 классник господи я и сейчас справляюсь с тупизной а что будет тогда?
я зашёл то сюда чисто из интереса посмотреть ваши примеры но блин...
это знак- изучать посерьезнее сейчас. сайт Знания поможет вам не просто списывать, а понимать/разбирать темы
Ответ дал:
1
Ответ:
а)
б)
в)
г)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад