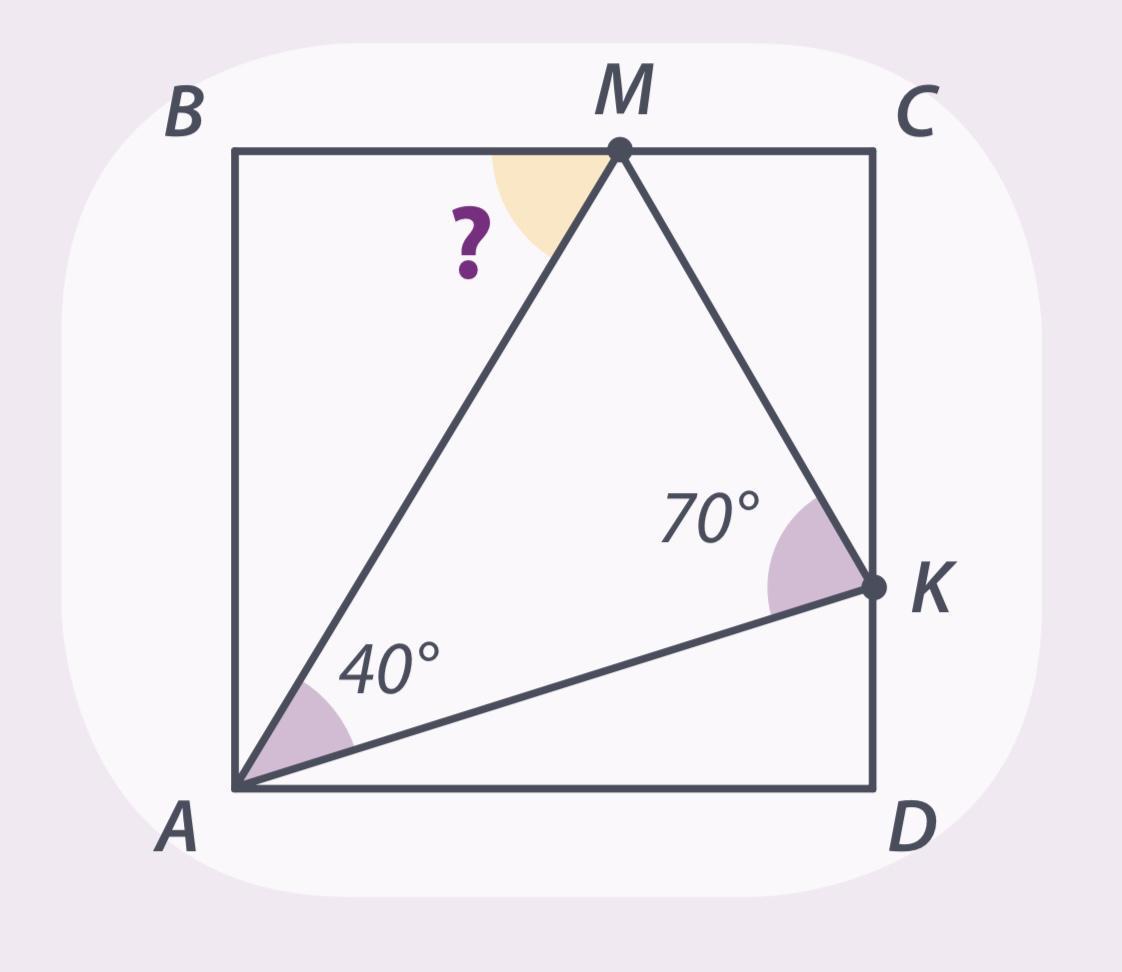
На сторонах ВС и СD квадрата АВСD взяли 24 точки М и К так, что угол КАМ равен 40°, а
угол АКМ равен 70°. Найдите угол АМВ.
Приложения:
kucerovanasta81:
Извини,а это задание за какой класс?
за 8 класс
Ответы
Ответ дал:
7
Ответ: 65°
Объяснение:
очевидно, что уголАМК=70° (треугольник АМК -равнобедренный);
следовательно, прямоугольные треугольники АВМ и АDК равны по гипотенузе (АМ=АК) и катету (АВ=АD);
из этого следует, что ВМ=DК и следовательно СМ=СК,
т.е. прямоугольный треугольник СМК -равнобедренный и уголСМК=45°...
и тогда уголВМА=180°-70°-45°=65°...
или так: из равенства треугольников АВМ и АDК следует: уголМАВ = уголКАD = (90°-40°)/2 = 25°
и т.к. сумма острых углов прямоугольного треугольника равна 90°, то уголАМВ=90°-25°=65°
боже, спасибо огромное
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад