Нужно упростить, а затем найти допустимые значения 'a' для данного выражения.
Я сделал, но ответ не совсем точный, если кто понимает, помогите разобраться!
Приложения:
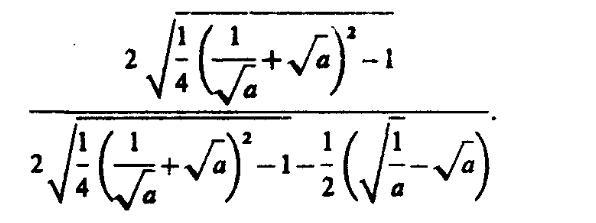

lidiasaraa3:
а что в ответе?
при a(0; 1)=> 2/3; a(1; +беск)=>2
Возможно я со знаками напортачил, на последнем этапе.
Ответы
Ответ дал:
1
Ответ:
a>1
Объяснение:
После упрощений получится следующее
Допустимые значения для a:
- Так как а входит под знак корня, то a>=0
Если a<1 , то знаменатель найденного выражения равен 0, значит a>1, выражение превращается в
Проверяем себя с помощью Maxima
Приложения:

тут дело не в том чтобы упростить до конца, а в том чтобы найти допустимые значения 'a' для данного выражения.
Я же ответ написал, только вот мой ответ, не совпадает с ответ из книге, по которой я решаю, у автора ответ такой же в плане значений, но промежутки в которых эти значения лежат у нас разные. У него так: при a(0; 1)=> 2/3; a(1; +беск)=>2
Я двойку пропустил в условии. Будет так 2|a-1|/2|a-1|-(1-a). a(0;1)=>2 и a(1;беск)=>2/3
Думаю, что ошибка в ответе. Вычислил значение исходного выражения при a= 1/2 и получил 2, при a=2 получил 2/3
Может быть, я так же вычислил, и ответ такой же получился, как у тебя, но не сходится именно тогда, когда с промежутками работал.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад