Question

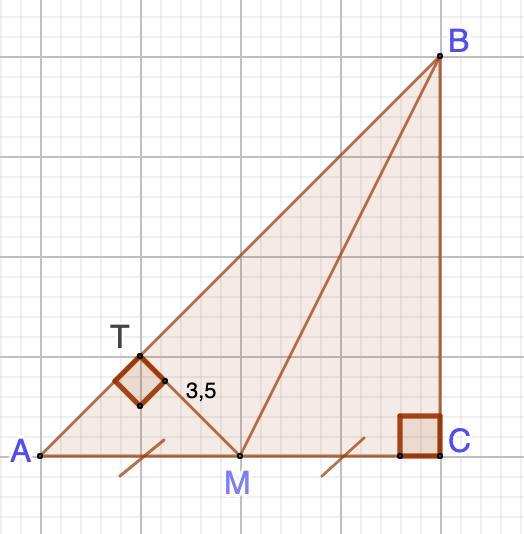
В равнобедренном прямоугольном треугольнике ABC с прямым углом C проведена медиана BM. Из точки M к гипотенузе восстановлен перпендикуляр MT . Найдите длину гипотенузы AB, если MT=3,5 .
CROCHNOOOOOOOOOOOO

Answer 1

Ответ:

АВ=14 (ед)

Объяснение:

Дано: ΔАВС - прямоугольный, равнобедренный.

ВМ - гипотенуза;

МТ⊥АВ

МТ=3,5

Найти: АВ

Решение:

1. Рассмотрим ΔАВС - прямоугольный, равнобедренный.

Углы при основании равнобедренного треугольника равны.

Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠А=∠В=90°:2=45°

2. Рассмотрим ΔАТМ - прямоугольный.

∠А=45° (п.1)

⇒ ∠АМТ=45° (сумма острых углов треугольника равна 90°)

⇒ ΔАТМ - равнобедренный (углы при основании равны)

АТ=ТМ=3,5

По теореме Пифагора:

$AM=\sqrt{AT^2+MT^2}=\sqrt{3,5^2+3,5^2}=3,5\sqrt{2}$

3. Рассмотрим ΔАВС

АС=ВС=2АМ=7√2 (ВМ - медиана)

По теореме Пифагора:

$AB=\sqrt{BC^2+AC^2}=\sqrt{98+98}=14$

АВ=14 (ед)