Помогите решить задачу))
2 стороны треугольника равны 12 см и 9 см,а угол между ними 30°.
Найдите площадь треугольника.
Ответы
Ответ дал:
0
Ответ дал:
0
что это?
Ответ дал:
0
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними
Ответ дал:
0
Площадь треугольника можно найти разными способами.
Найдем площадь по формуле
S=ah:2
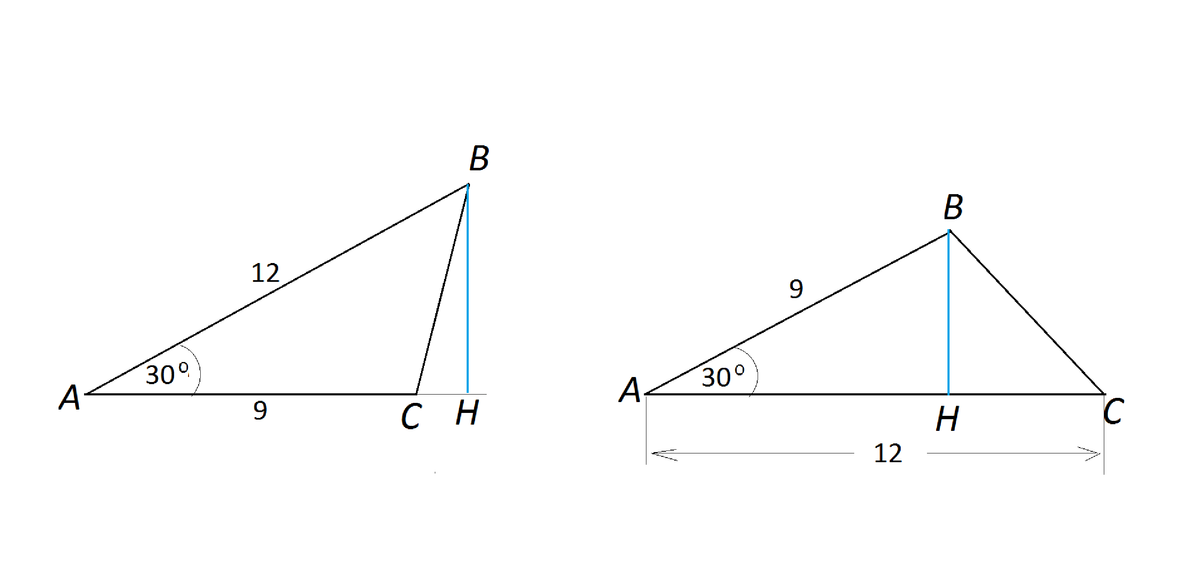
Вариант а):
АВ=12 см, АС=9 см, ∠ВАС=30°
Тогда высота
ВН=АВ:2, так как катет прямоугольного треугольника, противолежащий углу 30°, равен половине гипотенузы.
ВН=6 см
S=9·6:2=27cм²
Вариант б):
АВ=9см, АС=12 см, ∠ВАС=30° Высота
ВН=АВ:2=9:2=4,5 см
S=ВН*АС:2=4,5·12·2=27 см²
Найдем площадь по формуле
S=ah:2
Вариант а):
АВ=12 см, АС=9 см, ∠ВАС=30°
Тогда высота
ВН=АВ:2, так как катет прямоугольного треугольника, противолежащий углу 30°, равен половине гипотенузы.
ВН=6 см
S=9·6:2=27cм²
Вариант б):
АВ=9см, АС=12 см, ∠ВАС=30° Высота
ВН=АВ:2=9:2=4,5 см
S=ВН*АС:2=4,5·12·2=27 см²
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
11 лет назад