Ответы
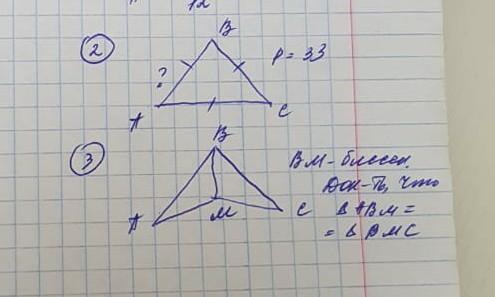
1) АВС - это равносторонний треугольник, все его стороны между собой раны, в таком случае, если Р=33, то АВ=ВС=СА=33:3=11.
2) Доказать, что ΔАВМ=ΔDMC, при биссектрисе ВМ.
Биссектриса ∠АВС - ВМ, выходящая из его вершины, делит этот внутренний угол треугольника на две равные половинки, то есть ∠ABM=∠MBC.
!Теперь внимание: исходя из данных только о биссектрисе BM, доказать, что треугольники ΔАВМ и ΔDMC равны - нельзя, по факту они разные. Поэтому предположу, что по условию стороны AB и BC были равны. Тогда:
AB = BC; BM - общая сторона в треугольниках ΔАВМ, ΔDMC; ∠ABM=∠MBC. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. ΔАВМ=ΔDMC по первому признаку равенства треугольников.