Здравствуйте. Ребят, подскажите, пожалуйста, формулу для вычисления сего чуда: y = lntgx^1/3. И фото, мало ли, ошибся в чём-то. Если не сложно, напишите, пожалуйста, что это такое в принципе. Лично я понимаю, что это логарифм тангенса в степени 1/3. Спасибо :)
Приложения:
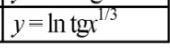
Ответы
Ответ дал:
1
Пошаговое объяснение:
Дружище, это функция, формулы вычисления её нету )
Вот график функции, если он вдруг зачем то тебе нужен
Приложения:

ckopo6ygy:
Благодарю)
Ответ дал:
1
Ответ:
Смотри разбор
Пошаговое объяснение:
Это сложная функция)
Немного непонятна просьба решения этого чуда, но, как я понял, Вас интересует нахождение корней.
n∈z
Благодарю)
Здесь не логарифм под кубическим корнем, если б он был под ним, тогда степень стояла бы после логарифма )
Даже если так, корни одинаковые
Нет
если тангенс в степени 1/3, то да
Да там x в степени 1/3 ,__,
Если логарифм то степень после логарифма, если тангенс, то после тангенса, но тут степень после x.....
по факту, но это уже какое то издевательство. зачем х в степень возводить? там же корни сумасшедшие получаюся
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад