Question

Срочно геометрия даю 30 балов

Квадрат ABCD і рівнобедренний трикутник KBC (KB=KC) лежать у різних площинах. Точки M і P середини відрізків BK i KC.
1)Визначте вид чотирикутника MPDA.
2)Визнаяте площу чотирикутника MPDA, якщо AB=12 см, MA=PD= 5см.

Answer 1

Ответ:

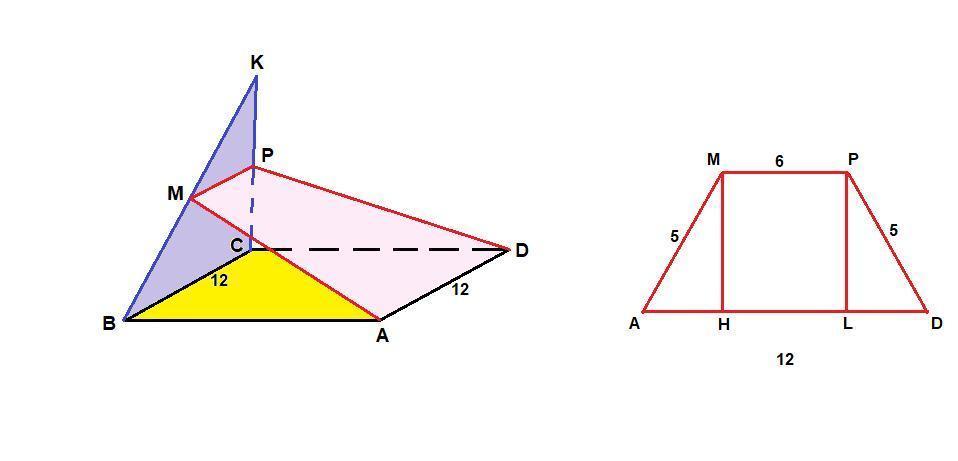
1) MPDA - равнобедренная трапеция

2) 36 см²

Объяснение:

1) МР - средняя линия треугольника ВСК, поэтому

МР║ВС и МР = 1/2 ВС = 6 см

МР║ВС, ВС║AD, ⇒ МР║AD.

Значит, MPDA трапеция. А так как МА = PD = 5 см, то

MPDA - равнобедренная трапеция.

2) Проведем высоты трапеции МН и PL. MPLH - прямоугольник, так как у него все углы прямые, тогда

HL = MP = 6 см.

ΔАМН = ΔDPL по гипотенузе и катету (∠АНМ = ∠DLP = 90°, так как проведены высоты, АМ = DP по условию и МН = PL как высоты), значит

АН = DL = (AD - HL)/2 = (12 - 6)/2 = 3 см

ΔАМН: прямоугольный, египетский, значит МН = 4 см.

Smpda = (MP + AD)/2 · MH = (6 + 12)/2 · 4 = 36 см²