Найдите угол между прямыми заданными уравнениями: б) х+у+1=0,х-у-1=0. Найдите эти прямые
это по геометрии
Ответы
Ответ дал:
2
Из уравнений прямых их направляющие вектора : и
. Найдём же угол между прямыми.
Ответ: , угол между прямыми измеряется от
до
Ответ дал:
0
Найдите угол между прямыми заданными уравнениями: б) х+у+1=0,х-у-1=0. Найдите эти прямые
Объяснение:
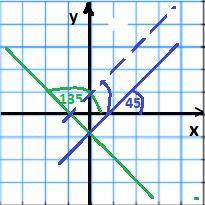
х+у+1=0 , у=-х-1 , к= -1 ⇒ tgα=-1 , α=135° это угол между прямой и положительным направлением оси ох
х-у-1=0 , у=х-1 , к= 1 ⇒ tgα= 1 , α=45° это угол между прямой и положительным направлением оси ох .
Значит угол между прямыми 135°-45° =90°
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад